Деление числа в данном отношении

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из 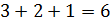 частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

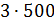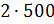– Тогда масса молока в смеси будет равна  и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна  и равна 1000 грамм, а масса сахара будет равна 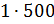 и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно 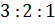. В таких случаях говорят, что число 3000 разделили в отношении 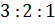. Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение 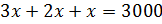. Решим это уравнение. Получим, что 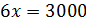. Отсюда 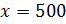. Тогда массы молока, сливок и сахара равны соответственно 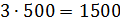 грамм, 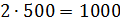 грамм и 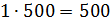 грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: разделите числа в указанных отношениях: а) число 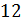 в отношении 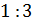;   б) число 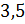 в отношении .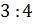

Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из 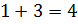 частей. Значит, 1 часть равна 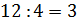. Тогда 3 части будут равны 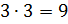. Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из 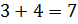 частей. Тогда 1 часть равна 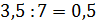. Отсюда 3 части числа равны 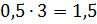. Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

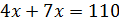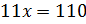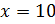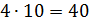Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .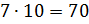

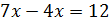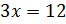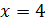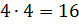Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .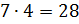

Решим задачу: стороны прямоугольника  относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

Решение: обозначим за х длины частей, из которых состоят стороны прямоугольника. Так как периметр прямоугольника равен удвоенной сумме длин его соседних сторон, то можем составить уравнение: . Решим уравнение. Получим . Отсюда . Следовательно, одна сторона прямоугольника равна  сантиметрам, вторая –  сантиметрам. Площадь прямоугольника равна произведению длин соседних сторон. Тогда площадь прямоугольника равна  см². Запишем ответ.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из 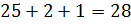 частей, имеющих одинаковые массы. Тогда 1 часть содержит 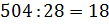 грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: 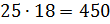 грамм белой глины, 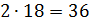 грамм песка и 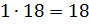 грамм гипса.

Не забудем записать ответ.