Остроугольный, прямоугольный и тупоугольный треугольники

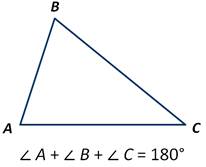
Теорема о сумме углов треугольника:

Сумма углов треугольника равна 180 градусов.

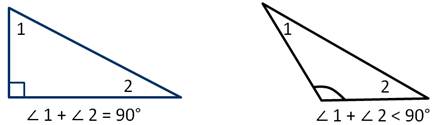
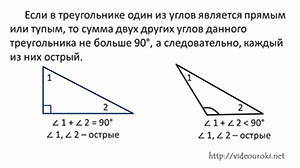
Из теоремы следует, что если в треугольнике один из углов является прямым или тупым, то сумма двух других углов данного треугольника не больше 90 градусов, а следовательно, каждый из них острый.

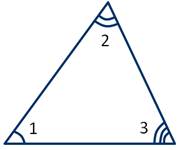
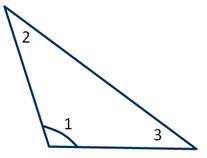
По величине углов выделяют следующие виды треугольников.

Определение:

Остроугольный треугольник - это треугольник, у которого все три угла острые.

Определение:

Тупоугольный треугольник - это треугольник, у которого один из углов тупой.

Определение:

Прямоугольный треугольник - это треугольник, у которого один из его углов является прямым.

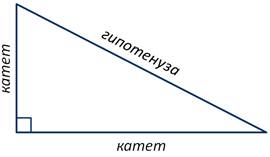
Нужно знать, что стороны прямоугольного треугольника имеют специальные названия.

Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

Если взять прямоугольный лист бумаги и разрезать его, получим:

Получим две модели прямоугольного треугольника.

Пример.

Доказать, что угол с вершиной на окружности, опирающийся на диаметр, - прямой.

Для начала соединим точку В с точкой О, которая является центром нашей окружности. Так как отрезки ОА, ОВ и ОС равны как радиусы окружности, то треугольники АОВ и ВОС являются равнобедренными. А значит, у них углы при основаниях равны. Обозначим градусные меры этих углов m и n. Тогда ∠АОВ=2n, так как он является внешним углом треугольника ВОС, смежным с ∠ВОС. А нам известно, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

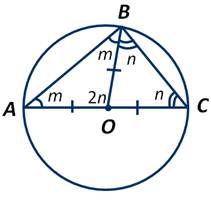
А так как сумма углов треугольника равна 180 градусов, то:

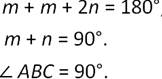
Что и требовалось доказать.

Пример.

Доказать, что если в равнобедренном треугольнике АВС один из углов равен 60 градусов, то он равносторонний.

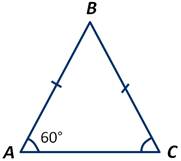
Если ∠А при основании равнобедренного треугольника АВС равен 60 градусов, то и второй ∠С при основании равен 60 градусам. Получаем:

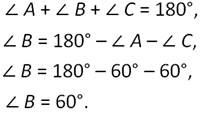
Следовательно, треугольник АВС равносторонний.

Пусть ∠В при вершине равнобедренного треугольника АВС равен 60 градусам. Тогда получим:

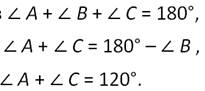
А так как углы А и С- углы при основании равнобедренного треугольника, то они равны между собой и равны 60 градусам. А следовательно, и в этом случае треугольник АВС является равносторонним. Что и требовалось доказать.

Пример.

Доказать, что в прямоугольном треугольнике АВС медиана, проведённая к гипотенузе АВ, равна половине гипотенузы.

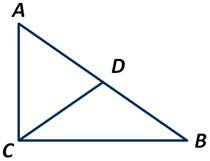
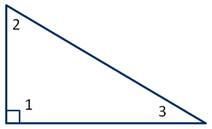
Отложив ∠2=∠1, получаем:

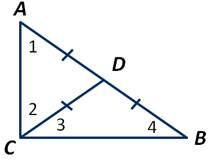
Треугольник ADC является равнобедренным. А следовательно, отрезок DA=DC.

Так как по условию угол АВС - прямой, то:

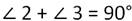
Известно, что сумма острых углов прямоугольного треугольника равна 90 градусов, то есть:

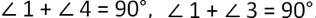
Тогда из равенств получаем:

Из этого следует, что ВСD равнобедренный треугольник, у которого стороны DB и DC равны.

Следовательно, СD - медиана и СD равняется половине гипотенузы АВ. Что и требовалось доказать.