Презентация к уроку математики "Графики с модулем"

По определению модуля, выражение y=|f(x)| равносильно системе    

              f(x),  если f(х)³0,

        Y=

              -f(x), если f(x)<0.

1) Для f(x) ≥ 0, |f(x)| = f(x)

 2) Для f(x) < 0, |f(x)| = -f(x)

 Симметричное  отображение части графика из нижней  полуплоскости в верхнюю относительно Ox.

Построения графиков функций вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.

Заметим, что в предыдущем примере  графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю.

Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями.

Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.

Подготовка к ГИА

Построение графиков функций, содержащих переменную под знаком модуля.

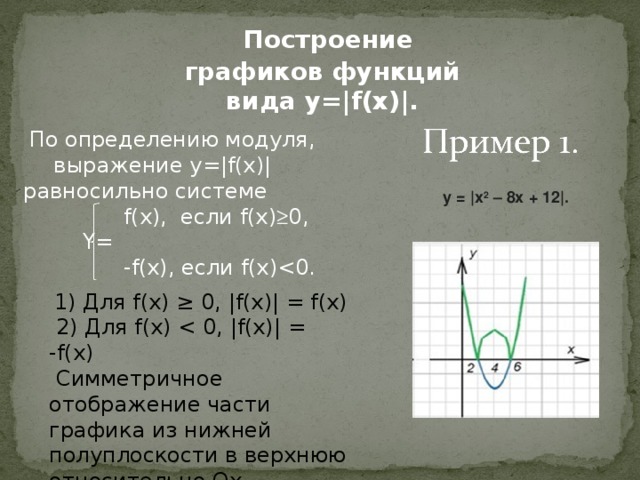
Построение графиков функций вида y=|f(x)|.

По определению модуля, выражение y=|f(x)| равносильно системе

f(x), если f(х)  0,

Y=

-f(x), если f(x)

y = |x 2  – 8x + 12|.

1) Для f(x) ≥ 0, |f(x)| = f(x)

2) Для f(x)

Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox

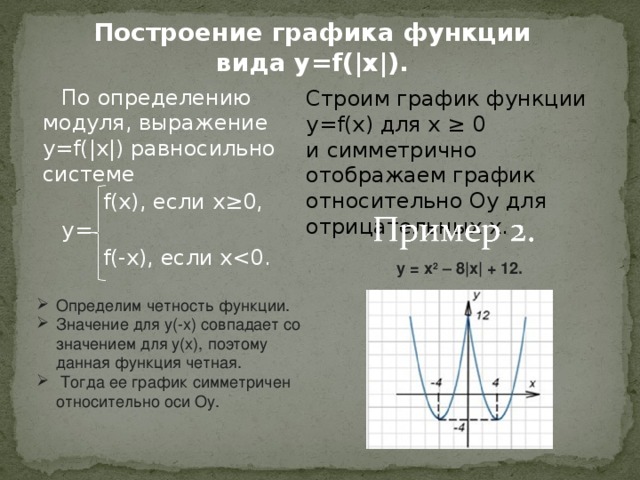
Построение графика функции вида y=f(|x|).

По определению модуля, выражение y=f(|x|) равносильно системе

f(x), если х≥0,

у=

f(-x), если х

Строим график функции y=f(x) для x ≥ 0

и симметрично отображаем график относительно Oy для отрицательных x.

y = x 2  – 8|x| + 12.

• Определим четность функции.
• Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная.
• Тогда ее график симметричен относительно оси Oy.

Построение графика функции вида Y=|f(X)|+|G(x)|.

• Для построения графика функций такого вида нужно найти нули каждой функции под знаком модуля и нанести их на координатную прямую.
• На каждом из полученных промежутков необходимо раскрыть модули по определению, т.е. в зависимости от знака функции под модулем на данном промежутке.
• Затем нужно построить каждую из полученных функций у на их области определения; полученный график - искомый.

Пример 3.

y = |x + 1| – |x – 2|.

3, при x ≥ 2;

y = 2x – 1, при -1 ≤ x

-3, при x

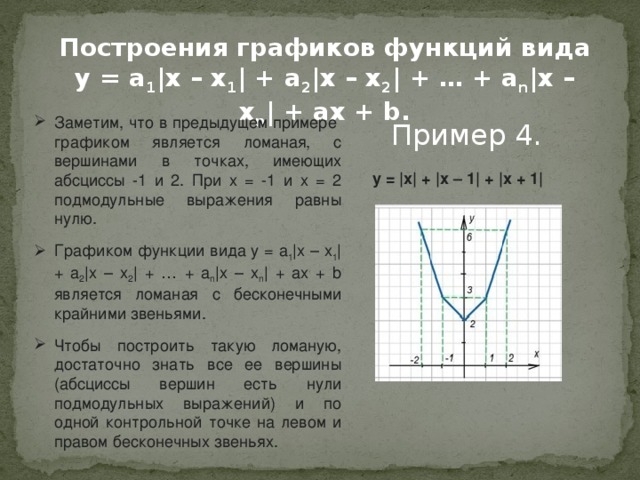
Построения графиков функций вида

y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b.

• Заметим, что в предыдущем примере графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю.
• Графиком функции вида y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b является ломаная с бесконечными крайними звеньями.
• Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.

Пример 4.

y = |x| + |x – 1| + |x + 1|

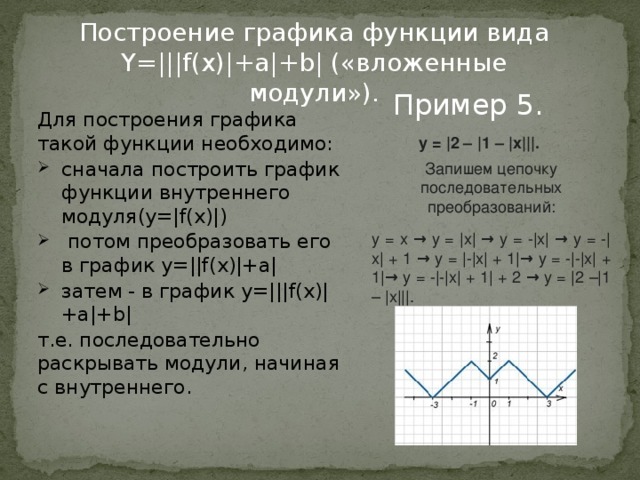
Построение графика функции вида Y=|||f(x)|+a|+b| («вложенные модули»).

Пример 5.

Для построения графика такой функции необходимо:

• сначала построить график функции внутреннего модуля(у=|f(x)|)
• потом преобразовать его в график у=||f(x)|+a|
• затем - в график у=|||f(x)|+a|+b|

т.е. последовательно раскрывать модули, начиная с внутреннего.

y = |2 – |1 – |x|||.

Запишем цепочку последовательных преобразований:

y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.

1; его растяжением в 1/а раз к оси у, если 1симметрией относительно оси х, если а" width="640"

Построение графика функции вида y=g(х)|f(x)|.

Если g(X)=a , то у=а|f(x)|. Тогда график функции у=а|f(x)| можно получить из графика функции у=|f(x)|

• его сжатием в а раз к оси у, если а1;
• его растяжением в 1/а раз к оси у, если 1
• симметрией относительно оси х, если а

Построение графика функции вида y=g(х)|f(x)|.

Пример 6.

Если g(x)  a , то

• находим нули функции под модулем и наносим их на координатную прямую.
• раскрываем модуль на получившихся промежутках по определению и перемножаем функции.

у=|х|(х+2).

Нуль функции f(x)=|х| х=0 делит координатную прямую на два промежутка - (-  ;0) и[0;+  ); на каждом из них раскроем модуль:

х 2 +2x, если х  0,

У=

-(х 2 +2х), если х

Построение графика функции вида |y|=f(x).

По определению модуля, выражение |у|=f(x) равносильно системе

y, если y  0,

f(x)=

-y, если у

Значит, чтобы построить график функции |у|=f(x), необходимо сначала построить график функции у=f(x), его часть, расположенную выше оси Х, оставить без изменений и , отбросив часть, расположенную ниже оси Х, отобразить симметрично относительно оси Х.

Пример 7.

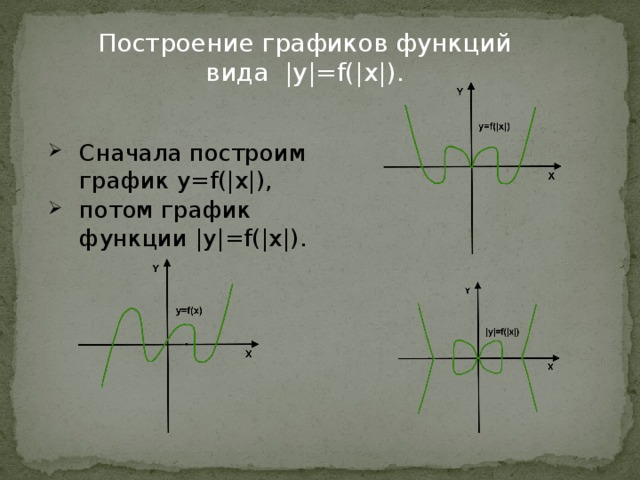
Построение графиков функций вида |y|=f(|x|).

• Сначала построим график y=f(|x|),
• потом график функции |y|=f(|x|).

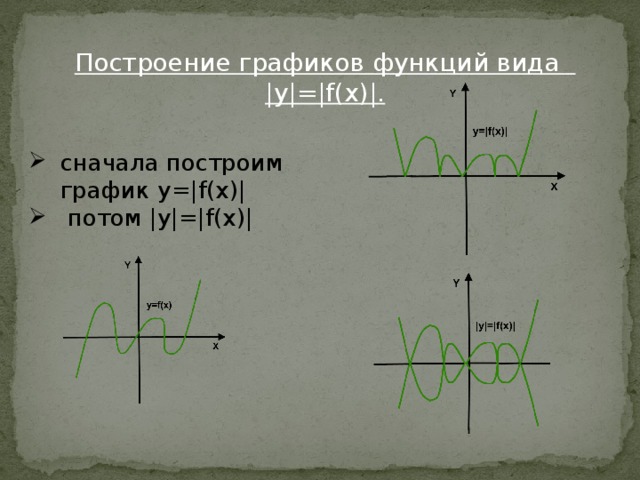
Построение графиков функций вида |y|=|f(x)|.

• сначала построим график y=|f(x)|
• потом |y|=|f(x)|