Презентация по математике на тему "Относительная частота случайного события"

В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

В классе учатся 16 мальчиков и12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?

Вода в реке Чумляк закипит.

Круглая отличница получит двойку.

В году найдется месяц, в котором будет пять воскресений.

Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило (m), к числу всех испытаний (n).

Полную информацию смотрите в файле.

Алгебра – 9 класс

28.04.

Относительная частота случайного события.

Автор: Спирина Ирина Марксовна, учитель математики МКОУ «Яланская СОШ» Курганская область

I категория

Устный счет

• Вычислить:

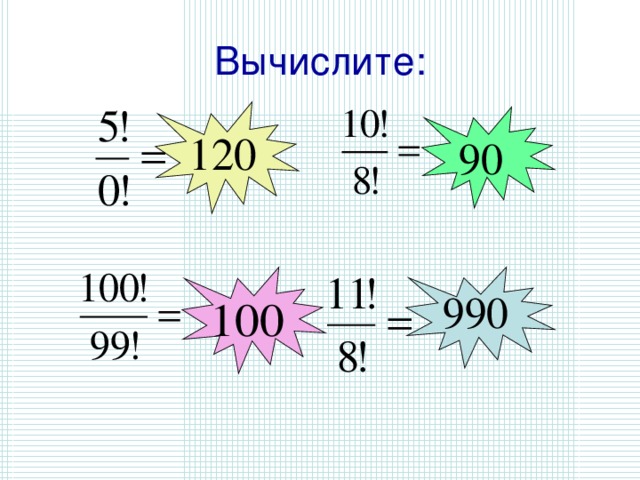
Вычислите:

Простейшие комбинации

Перестановки

Размещения

n элементов

n клеток

Сочетания

n элементов

k клеток

Порядок имеет значение

Порядок имеет значение

n элементов

k клеток

Порядок не имеет значения

……

……

……

В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Решение:

В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?

Решение:

Какое из перечисленных событий достоверное?

• Вода в реке Чумляк закипит.
• Круглая отличница получит двойку.
• В году найдется месяц, в котором будет пять воскресений.

Какое из перечисленных событий невозможно?

• В 12 часов ночи в Яланском идет дождь, а через 24 часа будет светить солнце.
• Сорванный цветок завянет.
• Если до воздушного шарика дотронуться иглой, то он лопнет.

Какое из данных событий случайное?

• Ударом молотка можно разбить стекло.
• Воробей научится говорить.
• Завтра будет хорошая погода.

Какое из данных событий более вероятное?

• В мае у нас пойдет снег.
• На день рождения тебе подарят подарок.
• В выходной день вы просыпаетесь, а на улице темно.

Какое из данных событий менее вероятное?

• Ты купил мороженое и выбросил его в урну.
• После четверга будет пятница.
• Новая электрическая лампочка не загорится.

Из данных событий выберете, то которое является равновозможным (равновероятным).

В коробке лежат 8 яблок и 5 лимонов.

• Из коробки вынут апельсин или лимон.
• Вынутый предмет будет яблоком или апельсином.
• Из коробки вынули апельсин или лимон.

На школьной олимпиаде по математике было предложено 5 заданий, Алеша выполнил 3,5 задания, а Игорь – 2 задания. У кого больше шансов стать победителем на школьной олимпиаде?

• У Алеши.
• У Игоря.

Что называется относительной частотой случайного события?

Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило ( m ) , к числу всех испытаний (n) .

Задача 1.

В денежно-вещевой лотерее на 100 000 билетов разыгрывается 1200 вещевых и 800 денежных выигрышей Какова относительная частота:

а) вещевого выигрыша;

0,012

б) денежного выигрыша;

0,008

Какова относительная частота какого-либо выигрыша?

0,02

Задача 2.

На учениях по стрельбе относительная частота поражения цели у рядового Петрова оказалось равной 0,8.

Сколько попаданий в цель можно ожидать от этого стрелка, если он произведет

20 выстрелов?

Задача 3.

Из деталей, лежащих в ящике три бракованные. Относительная частота появления бракованных деталей равна . Сколько всего деталей в ящике?