Презентация по математике на тему "Многогранники"

Человек проявляет  интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребёнка, играющего  деревянными кубиками, до зрелого  математика.

Особый интерес к правильным многоугольникам и правильным многогранникам связан с красотой и совершенством формы.

Увидеть их довольно просто: они окружают нас. В число правильных тел входят вирусы и простейшие организмы. Так же достаточно вспомнить форму снежинок, граней кристаллов,  ячеек в пчелиных сотах.  Ни одни геометрические тела не обладают таким совершенством и Ни одни геометрические тела не обладают такой красотой , как правильные многогранники.

Множество выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши, интересовались многогранниками и исследовали их.

Одним из основных вопросов, которыми они задавались, являлось число правильных многогранников.

Как много существует правильных многогранников?

Существует всего пять видов таких многогранников.

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n-угольники при n≥6.

Многогранники МБУ гимназия №35 г.о.Тольятти Самарской области

Правильный многогранник  или  платоново тело  — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

Человек проявляет  интерес к многогранникам на протяжении

всей своей сознательной деятельности – от двухлетнего ребёнка,

играющего  деревянными кубиками, до зрелого  математика.

Особый интерес к правильным многоугольникам и правильным

многогранникам связан с красотой и совершенством формы.

Увидеть их довольно просто: они окружают нас. В число правильных

тел входят вирусы и простейшие организмы.

Так же достаточно вспомнить форму снежинок, граней кристаллов,

ячеек в пчелиных сотах.  Ни одни геометрические тела не обладают

таким совершенством и Ни одни геометрические тела не обладают

такой красотой , как правильные многогранники.

Множество выдающихся мыслителей, от Платона и Евклида до

Эйлера и Коши, интересовались многогранниками и исследовали их.

Одним из основных вопросов, которыми они задавались, являлось

число правильных многогранников.

Как много существует правильных многогранников?

Существует всего пять видов таких многогранников.

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n-угольники при n ≥6.

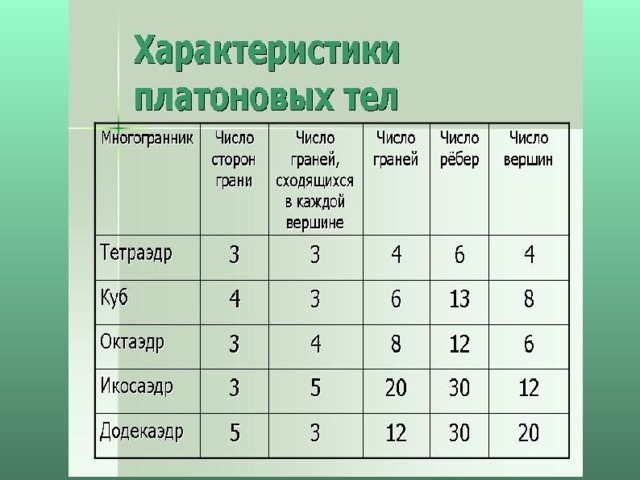
Правильные многогранники (Платоновы тела)

Гипотеза Платона

Итак, правильных многогранников Платон знал пять, а число стихий (огонь, воздух, вода и земля) было ровно четыре. Следовательно, из пяти многогранников надо выбрать четыре, которые можно было бы сопоставить со стихиями. Итак, тетраэдр символизировал огонь, т.к. его вершина устремлена вверх. Куб или гексаэдр символизировал – землю, как самый "устойчивый". Октаэдр символизирует воздух, как самый "воздушный". Икосаэдр символизирует – воду, т.к. он самый "обтекаемый". И всей вселенной была приписана форма додекаэдра, т. е. мы живём внутри небесного свода.

Тетраэдр - огонь

куб-земля

октаэдр-воздух

икосаэдр-вода

додекаэдр-вселенная

Математики говорили, что пчёлы

строили свои шестиугольные соты

задолго до появления человека.

Если разрезать пчелиные соты

плоскостью, то станет видна

сеть равных друг другу

правильных шестиугольников.

Из правильных многоугольников

с одинаковой площадью

наименьший периметр именно

у правильных шестиугольников.

Значит мудрые пчёлы экономят

воск и время для постройки сот.

Общая часть ячеек

является ромбом

Почему пчёлы строят соты именно так?

• Шестиугольная форма сотов объясняется не только мастерством пчел-строителей, но и простым физическим явлением. Структура сотов, имеющих форму правильных шестиугольников, обеспечивает им достаточно высокую прочность при минимальной толщине стенок и является оптимальной для хранения меда: шестигранные соты вмещают больше меда, чем могли бы вместить трех- или четырехгранные, изготовленные из того же количества воска.
• Но как же пчелам удается построить соты идеальной шестиугольной формы? Результаты исследования, проведенного недавно учеными из Китая и Великобритании, говорят о том, что пчелы изначально строят не шестиугольные, а круглые соты, запечатывая воском треугольные просветы на стыках их стенок.
• Дальше в дело вступают тепло тел рабочих пчел и физические свойства воска. При температуре около 45°C воск, превратившись в очень вязкую жидкость, начинает медленно течь. Силы поверхностного натяжения выдавливают воск из стыков стенок сотов, в результате чего стенки становятся плоскими, а сами соты – шестиугольными .

"Правильных многогранников вызывающе  мало,  - написал когда-то Л. Кэролл, - но этот весьма скромный по численности  отряд сумел пробраться в самые глубины различных наук".

Число многогранников

5

Однако сегодня историки математики предпочитают верить не Проклу, а обнаруженной схолии правильным телам в XIII книге «Начал» Евклида, где говорится, что Пифагор знал лишь три правильных тела — тетраэдр, гексаэдр (куб) и додекаэдр, а позднее Теэтет открыл и два оставшихся — октаэдр и икосаэдр.

По-видимому, сама природа подсказала пифагорейцам форму правильных тел: кристаллы поваренной соли имеют форму куба, кристаллы квасцов — октаэдра, а кристаллы пирита — додекаэдра. Последний, как показывают раскопки в Италии, был любимой игрушкой этрусских детей во времена Пифагора.

В самом деле, сумма плоских углов S при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m ≥ 3 . Значит, гранями правильных тел могут быть только три правильных

Док-во:

многоугольника: треугольник, квадрат и пятиугольник, ибо для шестиугольника

S =120°*3 = 360° . Из правильных треугольников можно составить три правильных тела:

m = 3 — тетраэдр, m = 4 — октаэдр и m = 5 — икосаэдр (при m = 6 S = 60 ° *6 = 360 ° ). Из квадратов и правильных пятиугольников — только по одному (куб и додекаэдр) при

m = 3 (при m = 4 S = 90° * 4 = 360° — для квадратов и S =108° * 4 = 432° — для пятиугольников).

Таким образом, правильных многогранников может быть только пять.

«Пифагор преобразовал геометрию, придав ей форму свободной науки, рассматривая ее принципы чисто абстрактным образом и исследуя теоремы с нематериальной, интеллектуальной точки зрения. Именно он нашел теорию иррациональных количеств и конструкцию космических тел». Так оценивал вклад Пифагора в геометрию Прокл, и эта оценка античного философа совершенно справедлива.

Прокл помимо замечательных открытий в планиметрии приписывает Пифагору построение всех пяти правильных тел.

В самом деле, в школе Пифагора геометрия оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически — как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию. При этом, что самое главное, свойства геометрических фигур устанавливались пифагорейцами не путем измерений, а с помощью логических доказательств.

Пифагорейцы проявляли повышенный интерес к правильным фигурам и телам.

Правильные геометрические формы благодаря их «правильности», т. е. наличию зеркальной или поворотной симметрии, как нельзя более отвечали всей пифагорейской философии о закономерном, структурно-упорядоченном гармоничном устройстве мироздания. Геометрические формы, в особенности правильные, наиболее выразительно выявляли число и как нельзя более подходили для «извлечения числа из вещей». Пифагорейцы раскладывали одни геометрические формы на другие какие-либо и в этом видели постижение внутренней взаимосвязи явлений.

Особенности

Пифагорейцы заметили, что в кубе число вершин (8) есть среднее гармоническое числа граней (6) и числа ребер (12) и поэтому называли куб гармоническим телом. Особое

предназначение куба виделось также и в том, что он единственный из правильных тел сплошь заполняет пространство.

Ко времени Евклида было замечено, что куб и октаэдр, а также додекаэдр и икосаэдр дуальны , т. е. число граней одного тела равно числу вершин другого и наоборот. Тогда одно тело может быть получено из другого, если центры тяжести граней одного принять за вершины другого или наоборот. Тетраэдр дуален сам себе.

Однако важнейшее свойство выпуклых многогранников было установлено лишь в середине XVIII в. теоремой Эйлера : во всяком выпуклом многограннике число вершин ( L ) плюс число граней ( M ) минус число ребер ( N ) есть величина постоянная, равная двум:

L + M − N = 2

Симметрия

ПРАВИЛЬНЫЙ ТЕТРАЭДЕР не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

КУБ имеет центр симметрии - центр куба, 9 осей и плоскостей симметрии

ПРАВИЛЬНЫЙ ОКТАЭДР имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии

ПРАВИЛЬНЫЙ ИКОСАЭДР имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии

ПРАВИЛЬНЫЙ ДОДЕКАЭДР имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

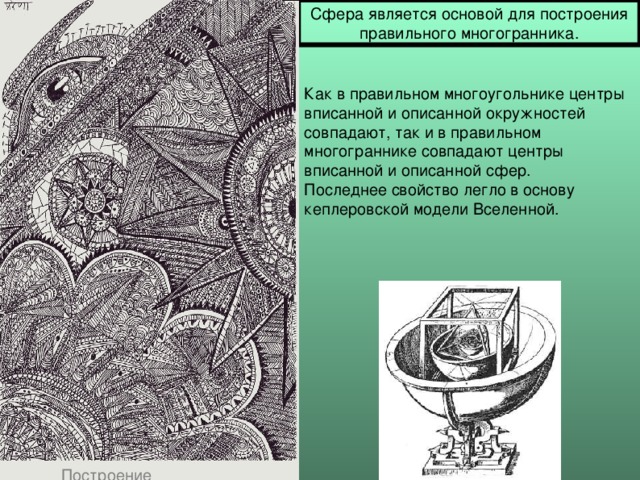
Сфера является основой для построения правильного многогранника.

Как в правильном многоугольнике центры вписанной и описанной окружностей совпадают, так и в правильном многограннике совпадают центры вписанной и описанной сфер.

Последнее свойство легло в основу кеплеровской модели Вселенной.

Построение

Учение о числе.

Числа древними греками, а вместе с ними Пифагором и пифагорейцами мыслились зримо, в виде камешков37, разложенных на песке или на счетной доске — абаке. По этой причине греки не знали нуля, так как его невозможно было «увидеть». Но и единица еще не была полноправным числом, а представлялась как некий «числовой атом», из которого образовывались все числа. Пифагорейцы называли единицу «границей между числом и частями», т. е. между целыми числами и дробями, но в то же время видели в ней «семя и вечный корень». Число же определялось как множество, составленное из единиц .

Особое положение единицы как «числового атома» роднило ее с точкой, считавшейся «геометрическим атомом». Вот почему Аристотель писал: «Точка есть единица, имеющая положение, единица есть точка без положения». Итак, пифагорейские числа в современной терминологии — это натуральные числа.

Числа-камешки раскладывались в виде правильных геометрических фигур, эти

фигуры классифицировались. Так возникли числа, сегодня именуемые фигурными : линейные числа (т. е. простые числа) — числа, которые делятся только на единицу и на самих себя и, следовательно, представимы в виде последовательности точек,

выстроенных в линию: - линейное число 5

Представление чисел в виде правильных геометрических фигур помогало пифагорейцам находить различные числовые закономерности.

Именно от фигурных чисел пошло выражение: «Возвести число в квадрат или куб».

Кристаллическая решетка поваренной соли имеет кубическую структуру.

Кристаллы в форме октаэдра

Квасцы

Шпинель

Флюорит

Алмаз

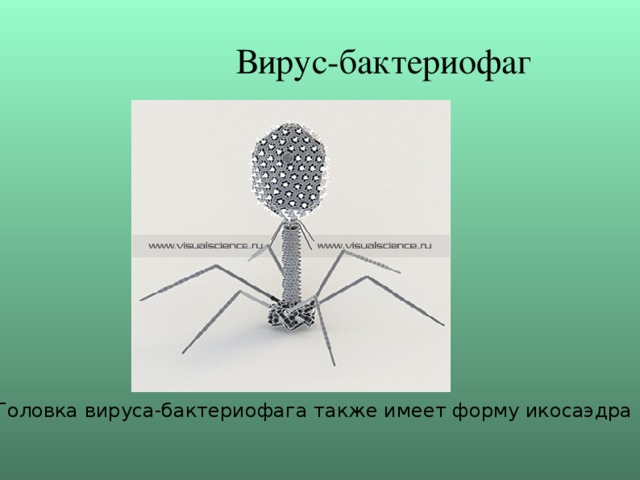
Вирус-бактериофаг

Головка вируса-бактериофага также имеет форму икосаэдра

Кристаллы в форме призм

Рубин

Горный хрусталь

Благодарим за внимание! Учитель математики Батаева Г.А.