Муниципальное бюджетное образовательное учреждение
дополнительного образования детей дом детского творчества
г. Зверева Ростовской области
Алгебраические уравнения.
Работа педагога дополнительного
образования
Куца Фёдора Ивановича
г. Зверево
2014г.
Алгебраическим уравнением n- й степени называется уравнение a0 xn + a1 xn- 1 + ∙∙∙ + an- 1 x + an.
Cодержание:
1) Биквадратные уравнения.
2) Возвратные уравнения третьей степени.
3) Возвратные уравнения четвертой степени.
4) Обобщенные возвратные уравнения четвертой степени.
5) Метод неопределенных коэффициентов.
6) Решение уравнений с помощью формулы a2 - b2 = (a + b)(a - b).
7) Решение уравнений относительно коэффициентов.
8) Следствие из теоремы о корнях многочлена.
9) Следствие из теоремы о многочленах, деление углом.
10) Использование схемы Горнера.
11) Использование формулы суммы бесконечно убывающей геометрической прогрессии.
12) Замена переменных по явным признакам.
13) Уравнения вида А4(х) + В4(х) = С.
14)Использование однородности.
1) Биквадратные уравнения.
Биквадратным называется уравнение вида ах4 +bх2 + с = 0.
Биквадратные уравнения решаются методом введения новой переменной: положив x2 = t (t 0)
придём к квадратному уравнению at2 + bt + c = 0.
Пример 1. 2х4 + 3х2 - 5 = 0.
Решение. Введем новую переменную x2 = t, где t 0, получим уравнение 2t2 + 3t -5 = 0.
Решив его, получим корни: t1 =1, t2 = - 5.
t2 = - 5 условию t 0 не удовлетворяет.
Далее решаем уравнение х2 = 1, его корни х1,2 = ± 1.
Ответ: х1,2 = ± 1.
Пример 2. 4х4 - 17х2 -15 = 0.
Решение. Введем новую переменную x2 = t, где t 0, получим уравнение 4t2 - 17t - 15 = 0.
D = b2 - 4ac = (- 17)2 - 4∙4∙ (- 15) = 529.
t1,2 = 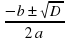 =
=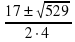 =
=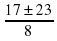 .
.
t1 = 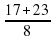 =
= 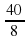 = 5;
= 5;
t2 =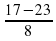 = -
= - 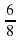 = -
= -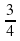 условию t 0 не удовлетворяет.
условию t 0 не удовлетворяет.
Далее решаем уравнение х2 = 5, его корни х1,2 = ± 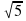 .
.
Ответ: х1,2 = ± 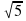 .
.
Пример 3. х4 - 37х2 + 36 = 0.
Решение. Введем новую переменную x2 = t, получим уравнение t2 - 37t + 36 = 0.
Решив его, получим корни: t1 =1, t2 = 36.
Далее решаем уравнения: 1) х2 = 1, х1,2 = ± 1.
2) х2 = 36, х1,2 = ± 6.
Ответ: х1,2 = ± 1; х3,4 = ± 6.
Пример 4. х4 + 37х2 +36 = 0.
Решение. Введем новую переменную x2 = t, где t 0, получим уравнение t2 + 37t + 36 = 0.
Решив его, получим корни: t1 = -1, t2 = -36; которые не удовлетворяют условию t 0, следовательно, исходное уравнение корней не имеет.
Ответ. Корней нет.
2) Возвратные уравнения третьей степени.
Возвратным называется уравнение вида: ах3 + bх2 + bх + а = 0.
Метод решения: разложение на множители способом группировки.
Пример 5 . 2х3 + 7х2 + 7х + 2 = 0.
Решение. (2х3 + 2) + (7х2 + 7х) = 0;
2 (х3 + 1) + 7х (х + 1) = 0;
2(х + 1) (х2 - х + 1) + 7х (х + 1) = 0;
(х+1)(2х2 - 2х + 2 + 7х) = 0;
(х+1)(2х2 + 5х + 2) = 0.
х+1 = 0 или 2х2 + 5х + 2 = 0,
х = -1. х1,2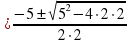 =
= 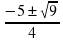 =
=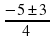 ,
,
х1 = -2, х2 = - 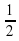 .
.
Корни исходного уравнения: х1 = -2, х2 = -1, х3 = - 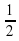 .
.
Ответ: х1 = -2, х2 = -1, х3 = - 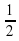 .
.
3) Возвратные уравнения четвертой степени.
Возвратным называется уравнение вида: ах4 + bх3 + сх2 ± bх + а = 0.
х = 0 не является корнем данного уравнения, поэтому можно разделить уравнение на х2 без потери корней, при этом получаем уравнение ах2 + bх + с ± 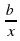 +
+ 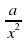 = 0, которое сводится к квадратному заменой х ±
= 0, которое сводится к квадратному заменой х ± 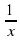 = t.
= t.
Пример 6. х4 - 2х3 - 22 х2 - 2х + 1 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнение на х2: х2 - 2х - 22 - 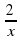 +
+ 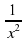 = 0; (х2 +
= 0; (х2 + 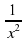 ) - 2∙(х +
) - 2∙(х + 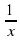 ) - 22 = 0.
) - 22 = 0.
Сделаем замену х + 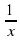 = t, тогда х2 + 2 +
= t, тогда х2 + 2 + 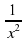 = t2, откуда х2+
= t2, откуда х2+ 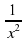 = t2 - 2 и уравнение сводится к виду: t2 - 2 - 2t - 22 = 0 , т.е. t2- 2t - 24 = 0, откуда t1 = 6, t2 = - 4.
= t2 - 2 и уравнение сводится к виду: t2 - 2 - 2t - 22 = 0 , т.е. t2- 2t - 24 = 0, откуда t1 = 6, t2 = - 4.
Возвращаясь к переменной х, рассмотрим два случая:
1) х + 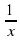 = 6, откуда х2 - 6х + 1 = 0, х1,2 = 3 ±
= 6, откуда х2 - 6х + 1 = 0, х1,2 = 3 ±  .
.
2) х + 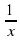 = - 4, откуда х2 + 4х + 1 = 0, х1,2 = - 2 ±
= - 4, откуда х2 + 4х + 1 = 0, х1,2 = - 2 ±  .
.
Корни исходного уравнения: х1,2 =3 ±  , х3,4 = - 2 ±
, х3,4 = - 2 ±  .
.
Ответ: х1,2 =3 ±  , х3,4 = - 2 ±
, х3,4 = - 2 ±  .
.
Пример 7. 2х4 - 15х3 +14 х2 + 15х + 2 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнение на х2: 2х2 - 15х + 14 +  +
+  = 0; 2 (х2+
= 0; 2 (х2+  ) - 15(х -
) - 15(х - 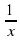 ) + 14 = 0.
) + 14 = 0.
Сделаем замену x -  = t, тогда х2 - 2 +
= t, тогда х2 - 2 +  = t2, откуда х2 +
= t2, откуда х2 +  = t2 + 2 и данное уравнение сводится к виду 2(t2 + 2) - 15t + 14 = 0 , т.е. 2t2- 15t + 18 = 0.
= t2 + 2 и данное уравнение сводится к виду 2(t2 + 2) - 15t + 14 = 0 , т.е. 2t2- 15t + 18 = 0.
D = b2 - 4ac = (-15)2 - 4∙2∙18 = 225 - 144 = 81.
х1,2 = 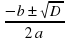 =
= =
= .
.
х1 = =
= = 6, х2 =
= 6, х2 =  =
= =
=  .
.
Возвращаясь к переменной х, рассмотрим два случая:
1) х - 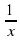 = 6, откуда х2 – 6х - 1 = 0, х1,2 = 3 ±
= 6, откуда х2 – 6х - 1 = 0, х1,2 = 3 ±  .
.
2) х - 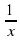 =
=  , откуда 2х2 - 3х - 2 = 0, х1 = 2, х2 = -
, откуда 2х2 - 3х - 2 = 0, х1 = 2, х2 = - 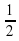 .
.
Корни исходного уравнения: х1,2 =3 ±  , х3 = 2, х4 = -
, х3 = 2, х4 = - 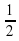 .
.
Ответ: х1,2 =3 ±  , х3 = 2, х4 = -
, х3 = 2, х4 = - 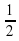 .
.
4) Обобщенные возвратные уравнения четвертой степени.
Обобщенным возвратным называется уравнение вида: ах4 + bх3 + сх2 ± dх + e = 0,
где  =
=  .
.
Пример 8. 3x4 - 2x3 - 31x2 + 10x +75 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнения на х2: 3x2 - 2x - 31 +  +
+ = 0; (3x2 +
= 0; (3x2 + ) - (2x -
) - (2x -  ) - 31 = 0; 3(x2 +
) - 31 = 0; 3(x2 + ) - 2(x -
) - 2(x -  ) - 31 = 0.
) - 31 = 0.
Пусть t = x -  , тогда t2 = х2 - 10 +
, тогда t2 = х2 - 10 +  , откуда x2 +
, откуда x2 + = t2 + 10 и данное уравнение сводится к виду: 3(t2 +10) - 2t – 31 = 0, т. е. 3t2 - 2t - 1 = 0.
= t2 + 10 и данное уравнение сводится к виду: 3(t2 +10) - 2t – 31 = 0, т. е. 3t2 - 2t - 1 = 0.
t1= 1, t2 = -  .
.
Возвращаясь к переменной х, рассмотрим два случая:
1) x -  = 1, откуда x2 - x - 5 = 0.
= 1, откуда x2 - x - 5 = 0.
х1,2=  .
.
2) x -  = -
= -  , откуда 3x2 + x - 15 = 0.
, откуда 3x2 + x - 15 = 0.
х1,2=  .
.
Корни исходного уравнения: х1,2 , х3,4 =
, х3,4 =
Ответ: х1,2 , х3,4 =
, х3,4 =
5) Метод неопределенных коэффициентов.
Пример 9. х4 – 5х3 + 8х2 – 5х + 1 = 0.
Решение. Представим многочлен, стоящий в левой части уравнения в виде произведения квадратных трехчленов: х4 - 5х3 + 8х2 - 5х + 1= (x2 + ax + b)(x2 + cx + d),где a,b,c,d-целые числа.
Раскрыв скобки и приведя подобные, имеем:
х4 - 5х3 + 8х2 - 5х +1 = x4 + (c + a)x3 + (ac + b + d)x2 + (ad + cb)x + bd.
или
х4 – 5х3 +8х2 – 5х +1 = (х2 – 2х + 1)(х2 – 3х + 1); (х2 – 2х + 1)(х2 – 3х + 1) = 0.
х2 – 2х + 1 = 0 или х2 – 3х + 1 = 0.
1) х2 – 2х + 1 = 0; (х – 1)2 = 0; х = 1.
2) х2 – 3х + 1 = 0; х1,2 = 
Корни исходного уравнения: х1 = 1, х2,3 .
.
Ответ: х1 = 1, х2,3 .
.
6) Решение уравнений с помощью формулы a2 - b2 = (a + b)(a - b).
Пример 10. x4 + 4x3 + 3x2 + 2x - 1 = 0.
Решение. x4 + 4x3 + 4x2 - x2 + 2x - 1 = 0; (x2 + 2x)2 - (x - 1)2 = 0;
(x2 + 2x - x + 1) (x2 + 2x + x - 1) = 0; (x2 + x + 1) (x2 + 3x - 1) = 0.
x2 + x + 1= 0 или x2 + 3x - 1 = 0.
D = 12 - 4∙ 1∙1 = - 3 1,2=  .
.
Корни исходного уравнения: х1,2
 .
.
Ответ: х1,2
 .
.
7) Решение уравнений относительно коэффициентов.
Пример 11. х6 - 7х2 +  = 0.
= 0.
Решение. x = 0 не является корнем данного уравнения.
х6 -  х2 +
х2 +  = 0; х6 - х2
= 0; х6 - х2  - х2 +
- х2 +  = 0; х2
= 0; х2  -
-  + х2 - х6 = 0.
+ х2 - х6 = 0.
a = х2, b = -1, c = х2 - х6
D = 1 - 4∙ х2∙ (х2 - х6) = 1- 4 х4 + 4х8 = (2x4- 1)2.
 =
=  или
или  =
=  .
.
I) 2 х2 =
х2 = 2
2 х2 =
х2 = ;
; + 2
+ 2 х2 - 2 = 0
х2 - 2 = 0 +
+  х2 - 1 = 0.
х2 - 1 = 0.
 =
=  или x2
или x2 =
= 
 =
=  не имеет корней, т.к.
не имеет корней, т.к.
 =
=  , следовательно, х1,2 = ±.
, следовательно, х1,2 = ±.
II) 2 х2 =х2 =
х2 =х2 = ;
; - 2
- 2 х2 = 0;
х2 = 0;
 -
-  х2 = 0;
х2 = 0;  -
-  х2 = 0.
х2 = 0.
 -
-  х2 = 0.
х2 = 0.
1)х1,2 = ±  = ±
= ± 
2) х = 0 (но x = 0 не является корнем исходного уравнения).
Корни исходного уравнения: х1,2 = ± , х 3,4 = ±  .
.
Ответ: х1,2 = ± , х 3,4 = ±  .
.
8) Следствие из теоремы о корнях многочлена.
Если многочлен с целыми коэффициентами имеет целые корни, то они являются делителями свободного члена.
Пример 12. х4 - 10х3 + 35х2 - 50х + 24 = 0.
Решение. Найдем корни подбором.
Делители свободного члена 24: ±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24.
Отрицательных корней уравнение не имеет, т.к. коэффициенты при нечетных степенях х – отрицательны.
Р4(1) = 14 - 10∙13 + 35∙12 - 50∙1 + 24 = 1 - 10 + 35 - 50 + 24 = 60 - 60 = 0, следовательно, х = 1 корень исходного уравнения.
Р4(2) = 24 - 10∙23 + 35∙22 - 50∙2 + 24 = 16 - 80 + 140 -100 + 24 = 180 - 180 = 0, значит, х = 2 корень исходного уравнения.
Р4(3) = 34 - 10∙33 + 35∙32 - 50∙3 + 24 = 81 - 270 + 315 - 150 + 24 = 420 - 420 = 0, поэтому х = 3 корень исходного уравнения.
Р4(4) = 44 - 10∙33 + 35∙42 - 50∙4 + 24 = 256 - 640 + 560 - 200 + 24 = 8400 - 840 = 0,х = 4 - корень исходного уравнения.
Так как корней не может быть больше, чем показатель многочлена, то все корни найдены.
Ответ: х1 = 1, х2 = 2, х3 = 3, х4 = 4.
9) Следствие из теоремы о многочленах, деление углом.
Пример 13. х3 - 7х + 6= 0.
Решение. Используя следствие из теоремы о многочленах: (Если сумма коэффициентов многочлена равна нулю, то один из корней равен единице).
Найдем сумму коэффициентов: 1 - 7 + 6 = 0 ,
Следовательно, х = 1 корень исходного уравнения.
Понизим степень уравнения, разделим многочлен х3 - 7х + 6 на двучлен х -1.
| х3 - 0х2 -7х + 6 - х3 - х2 | х - 1 |
| х2 + х - 6
|
|
0 | х2 -7х + 6 - х2 – х |
|
| -6х +6 - -6х +6 |
| 0 |
Решим теперь уравнение х2 + х - 6 = 0, его корни х1 = 2, х2 = -3.
Корни исходного уравнения х1 = 1, х2 = 2, х3 = -3.
Ответ: х1 = 1, х2 = 2, х3 = -3.
10) Использование схемы Горнера.
Пример 14. х4 + 3х3 + х2 – 3х – 2 = 0.
Решение. По следствию целые корни находятся среди делителей свободного члена.
Делители свободного члена - 2: ±1; ±2.Проверим по схеме Горнера каждое из них.
|
| 1 | 3 | 1 | -3 | -2 |
|
| 1 | 1 | 4 | 5 | 2 | 0 | корень |
| 1 | 1 | 5 | 10 | 12 |
| не корень |
| -1 | 1 | 3 | 2 | 0 |
| корень |
| -1 | 1 | 2 | 0 |
|
| Корень (кратности 2) |
х4 + 3х3 + х2 – 3х – 2 = (х -1) (х+1)2 (х+2)
Данное уравнение имеет 3 корня: х1 = 1,х2 = -1, х3 = 2, причем - 1 – корень кратности 2.
Ответ: х1 = 1, х2 = -1, х3 = 2.
11) Использование формулы суммы бесконечно убывающей геометрической прогрессии.
Пример 15. 2х + 1 + х2 – х3 + х4 – х5 + …=  , где |х|
, где |х|
Решение. Очевидно, что все слагаемые в левой части уравнения, не считая первых двух, образуют бесконечно убывающую геометрическую прогрессию с первым членом х2 и знаменателем (-х). Сумма этой прогрессии вычисляется по формуле S = =
=  =
=  .
.
Теперь исходное уравнение можно записать в виде 2х + 1 + =
=  ,
,
(2х +1)(х +1) + х2 =  (х+1), 3х2 + 3х +1 =
(х+1), 3х2 + 3х +1 =  (х +1), 6(3х2 + 3х +1) = 13 (х +1),
(х +1), 6(3х2 + 3х +1) = 13 (х +1),
18х2 + 18х + 6 = 13х +13, 18х2 + 5х - 7 = 0.
х1,2= =  .
.
х1 =  =
=  =
= 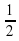 , х2 =
, х2 =  =
=  = -
= -  .
.
Ответ: х1 =
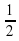 , х2 = -
, х2 = -  .
.
12) Замена переменных по явным признакам.
Пример 16. (х2 - 2х)2 - 2(х2 - 2х) - 3 = 0.
Решение. Введя новую переменную х2 - 2х = t, получим уравнение t2 - 2t - 3 = 0, решив
которое, имеем: t1 = - 1, t2 = 3.
Далее решаем уравнения: 1) х2 - 2х = - 1; х2 - 2х + 1 = 0; (х - 1)2 = 0; х = 1. 2) х2 - 2х = 3; х2 - 2х - 3 = 0; по т., обр.т. Виета: х1 = - 1, х2 = 3.
Ответ: х1 = 1; х2 = - 1, х3= 3.
Пример 17. (2х2 + 3х -1)2 - 10х2 - 15х + 9 = 0.
Решение. (2х2 + 3х -1)2 -10х2 -15х + 5 + 4 = 0;
(2х2 + 3х -1)2 -5(2х2 + 3х - 1) + 4 = 0.
Введем новую переменную 2x2 +3х -1= t, получим уравнение t2 -5t + 4 = 0.
Решив его, получим корни: t1 =1, t2 = 4.
Далее решаем уравнения: 1) 2x2 + 3х -1 = 1; 2x2 + 3х - 2 = 0,его корни х1 = - 2; х2 = 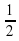 ,
,
2) 2x2 + 3х -1 = 4; 2x2 + 3х - 5 = 0,его корни х1 = 1; х2 = -  .
.
Корни исходного уравнения: х1 = 1; х2 = -2 х3 = 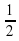 , х4 = -
, х4 = -  .
.
Ответ: х1 = 1; х2 = -2 х3 = 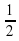 , х4 = -
, х4 = -  .
.
Пример 18. (х2 - 6х)2 - 2(х - 3)2 = 81.
Решение. Заметив, что х2 - 6х = (х - 3)2 - 9 и положив (х - 3)2 = у, где у ≥ 0, получим:
( у - 9)2 - 2у = 81, у2 - 18у + 81 - 2у - 81 = 0, у2 - 20у = 0, у (у - 20) = 0.
у1 = 0, у2 = 20.
Возвращаясь к переменной х, рассмотрим два случая:
1) (х - 3)2 = 0, х - 3 = 0, х = 3.
2) (х - 3)2 = 20, х - 3 = ± , х1,2 = 3 ±
, х1,2 = 3 ± .
.
Корни исходного уравнения: х1 = 3, х2,3 = 3 ± .
.
Ответ: х1 = 3, х2,3 = 3 ± .
.
13) Уравнения вида А4(х) + В4(х) = С.
Уравнения вида А4(х) + В4(х) = С решаются заменой t =  .
.
Пример 19. (х + 3)4 + (х + 1)4 = 20.
Решение. Введем замену t = = х + 2, тогда х = t – 2.
Сделаем замену (t +1)4 + (t -1)4 = 20.
Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:
t4 + 4t3 + 6t2 + 4t +1+ t4- 4t3 + 6t2 - 4t + 1 = 20.
Упростим уравнение, получим биквадратное уравнение относительно t:
2t4 + 12t2 - 18 = 0,
t4 + 6t2 - 9 = 0.
Пусть у = t2 , y 0, тогда t1,2 = ± .
.
у2 + 6у - 9 = 0, у1,2 = -3 ±  = -3 ± 3
= -3 ± 3 .
.
у1= -3 + 3 .
.
у2= -3 - 3 не удовлетворяет условию у 0.
не удовлетворяет условию у 0.
Следовательно, t1,2 = ± = ±
= ±
Откуда х1,2 = ± - 2.
- 2.
Ответ: х1,2 = - 2 ± .
.
14)Использование однородности.
Уравнения вида a∙A2(х)+ b∙A(х)B(х) + c∙B2(х) = 0 называются однородными.
I способ решения.
Введение новой переменной.
Пример 20. 3х2 + 4х( х2 + 3х + 4) + ( х2 + 3х + 4)2 = 0.
Решение. Введем новую переменную..
Пусть у = х2 + 3х + 4, тогда 3х2 + 4ху + у2 = 0.
Решаем относительно у: у1,2=  =
= ,
,
у1 = - х, у2 = -3х.
Следовательно: 1) х2 + 3х + 4 = - х, 2) х2 + 3х + 4 = - 3х,
х2 + 4х + 4 = 0, х2 + 3х + 4 + 3х = 0,
(х + 2)2 = 0, х2 + 6х + 4 = 0,
х = -2. х1,2 = -3 ±
Ответ: х1 = -2, х2,3 = -3 ±
II способ решения однородных уравнений.
Деление обеих частей уравнения на A2(х), A(х)B(х) или B2(х) и введение замены.
Пример 21. 2(х2 + х +1)2 - 7(х - 1)2 = 13(х3 - 1).
Решение. Так как х3 - 1 = (x2 + x + 1) (x - 1), a x2 + x + 1 ≠ 0 ни при каком х, то, разделив обе части данного уравнения на (х2 + х + 1)2 , получим:
2 - 7∙ = 13
= 13 .
.
Введем замену у =  , получим уравнение: 2 - 7у2 = 13у,
, получим уравнение: 2 - 7у2 = 13у,
7у2 + 13у - 2 = 0.
у1,2 = =  =
=  .
.
у1 = = - 2, у2 =
= - 2, у2 = =
=  ,.
,.
Возвращаясь к переменной х, рассмотрим два случая:
1) =
=  , 2)
, 2) = - 2,
= - 2,
7(х -1) = х2 + х + 1, х -1 = - 2(х2 + х + 1),
7х - 7 - х2 - х -1= 0, х -1 + 2х2 +2х + 2 = 0,
х2 - 6х + 8= 0. 2х2 +3х + 1 = 0,
х1 = 2, х2 = 4. х1 = - 1, х2 = - 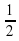 .
.
Ответ: х1 = 2, х2 = 4, х3 = - 1, х4 = - 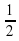 .
.
Пример 22. (х - 2)2(х + 1)2 - (х - 2)(х2 - 1) - 2(х - 1)2 = 0.
Решение. Число х = 1 не является корнем данного уравнения. Поэтому, поделив обе его части на
(х - 1)2, приходим к равносильному уравнению:
- 2 = 0. Сделав замену  = у, получим уравнение
= у, получим уравнение
у2 – у – 2 = 0, корни которого у1 = -1 , у2 = 2.
Возвращаясь к переменной х, рассмотрим два случая:
1) = - 1, = 2
= - 1, = 2
х2 - х - 2 = - х + 1, х2- х - 2 = 2х - 2,
х2 - 3 = 0, х2- 3х = 0,
х2 = 3, (х- 3)х = 0,
х1,2 = ± . х1 = 3, х2 = 0.
. х1 = 3, х2 = 0.
Ответ: х1,2 = ± , х3 = 3, х4 = 0.
, х3 = 3, х4 = 0.
15) Сумма квадратов равна нулю.
Пример 23. (х2 - 5х - 6)2 + (х2 + 3х +2)2 = 0.
Решение. Так как квадраты чисел - неотрицательны, то данная сумма квадратов равна нулю, если оба слагаемые равны нулю одновременно.
х = -1.
Ответ: х1= -1
Литература:
Математика. Большой справочник для школьников и поступающих в вузы. М."Дрофа",1999г.
Математика. Учебное пособие для слушателей подготовительных курсов. Новочеркасск. НГМА,2003г.
Алгебра и начала анализа.10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / Ш.А. Алимов и др/-М. просвещение,2010г.
Алгебра. ЕГЭ: шаг за шагом /А.А. Черняк, Ж.А.Черняк,- Волгоград: Учитель,2012.
Математика. ЕГЭ- 2006,вступительные экзамены. Пособие для самостоятельной подготовки. Ростов-на-Дону, Легион, 2005.

 Получите свидетельство
Получите свидетельство Вход
Вход



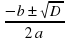 =
=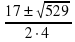 =
=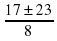 .
.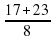 =
= 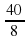 = 5;
= 5;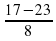 = -
= - 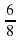 = -
= -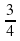 условию t 0 не удовлетворяет.
условию t 0 не удовлетворяет.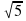 .
.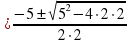 =
= 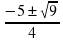 =
=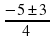 ,
,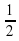 .
.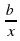 +
+ 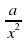 = 0, которое сводится к квадратному заменой х ±
= 0, которое сводится к квадратному заменой х ± 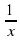 = t.
= t.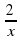 +
+ 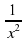 = 0; (х2 +
= 0; (х2 + 








 Алгебраические уравнения (52.61 КB)
Алгебраические уравнения (52.61 КB)
 0
0 1310
1310 47
47 Нравится
0
Нравится
0


