Численные методы математического программирования.
Нахождение приближенного значения площади криволинейной трапеции. Понятие интегрирования.
Потребность в приближенном вычислении площади криволинейной трапеции может возникнуть тогда, когда не существует или неизвестен метод отыскания точного значения площади фигуры, и тогда, когда этот метод известен, но неудобен.
Излагаемые приближенные численные методы основаны на следующем: рассматривая интегральные суммы для вычисления площади криволинейной трапеции, мы получим ее приближенное значение.
Существуют для этого случая два правила численного интегрирования: правило прямоугольников и правило трапеций.
Постановка задачи
Перед учащимися 11-го класса поставлена учебная задача: найти площадь фигуры, ограниченной сверху графиком функции 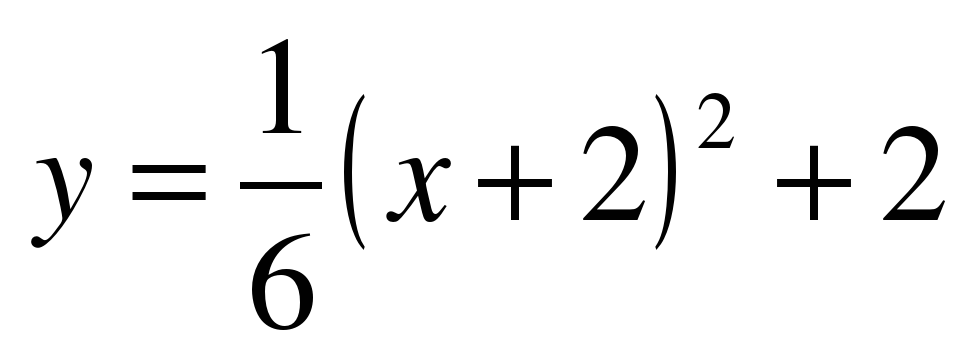 , отрезком [- 6; 3,5] оси Ox и вертикальными прямыми x=- 6, x=3,5, используя ранее полученные знания по теме «Площадь».
, отрезком [- 6; 3,5] оси Ox и вертикальными прямыми x=- 6, x=3,5, используя ранее полученные знания по теме «Площадь».
Проведя исследовательскую работу, учащиеся предложили следующие варианты решения этой проблемы:
Использование инструмента для измерения площадей плоских фигур – палетку.
Использование теоретических знаний по теме «Свойства площадей» и известных формул.
Использование формулы Пика: 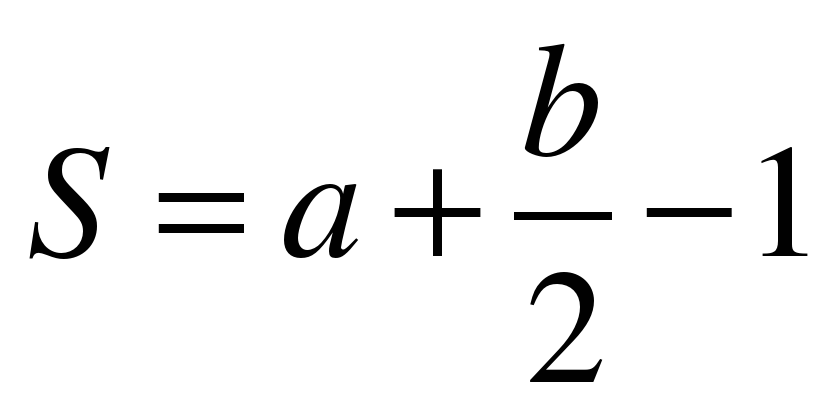 , подсчета числа узлов внутри многоугольника (a)и числа узлов на границе, включая вершины (b).
, подсчета числа узлов внутри многоугольника (a)и числа узлов на границе, включая вершины (b).
Обсудив полученные результаты, пришли к выводу, что использование известных учащимся методов, привело к результату, точность которого недостаточно высока.
Правило прямоугольников
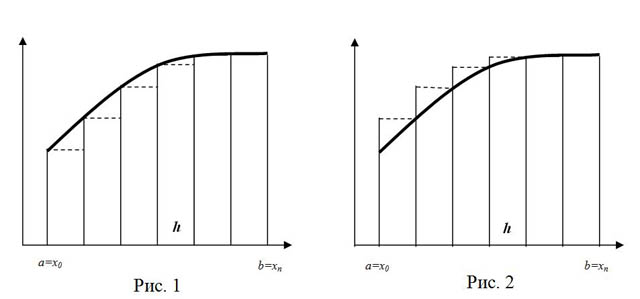
Разделим интервал интегрирования [a, b] на n равных частей (шагов) и заменим данную криволинейную трапецию ступенчатой фигурой, состоящей из n прямоугольников, опирающиеся на величину 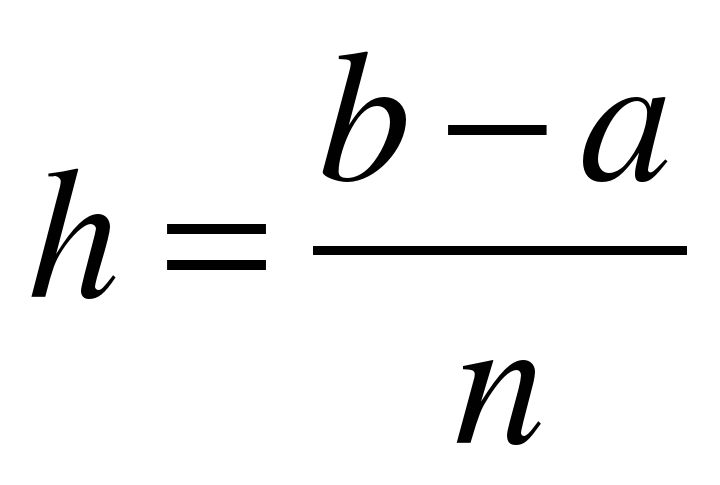 , которую назовем шагом, причем высоты этих прямоугольников равны значениям функции
, которую назовем шагом, причем высоты этих прямоугольников равны значениям функции 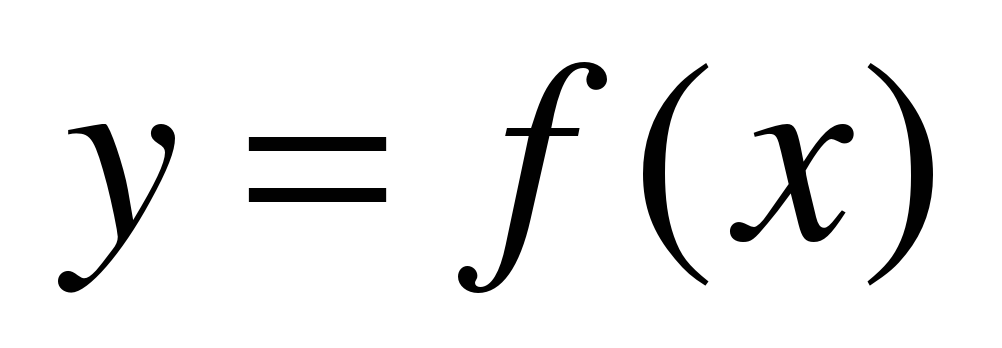 в начальных (рис. 1) или конечных (рис.2) точках величины
в начальных (рис. 1) или конечных (рис.2) точках величины 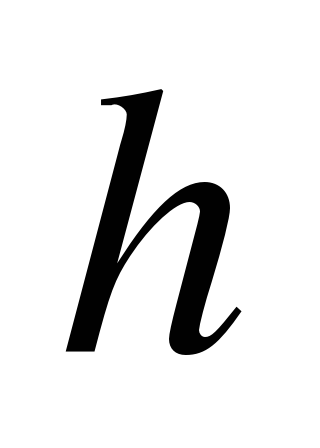 .
.
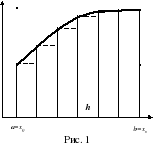
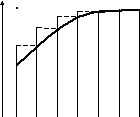
h

a=x0
b=xn
Рис. 2
Значение площади этой фигуры и будет давать приближенное значение искомого интеграла 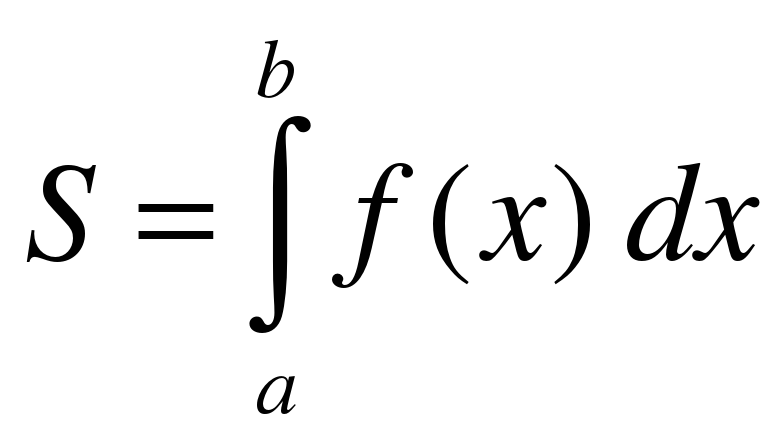 . Результат будет тем более точен, чем больше взято число шагов.
. Результат будет тем более точен, чем больше взято число шагов.
Если обозначить значения функции в точках деления через y0, y1,…,yn, то есть положить yk=f(xk), xk=a+kh, где 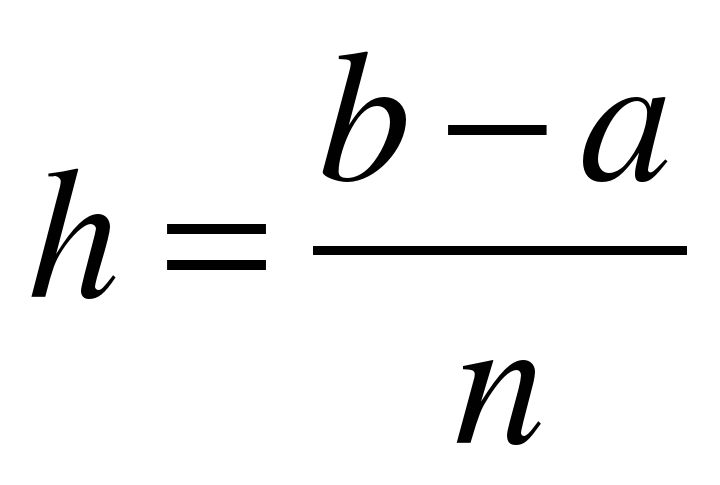 , а k принимает значение 0,1,2,…,n, то, очевидно, будем иметь следующие формулы:
, а k принимает значение 0,1,2,…,n, то, очевидно, будем иметь следующие формулы:
 (1)
(1)
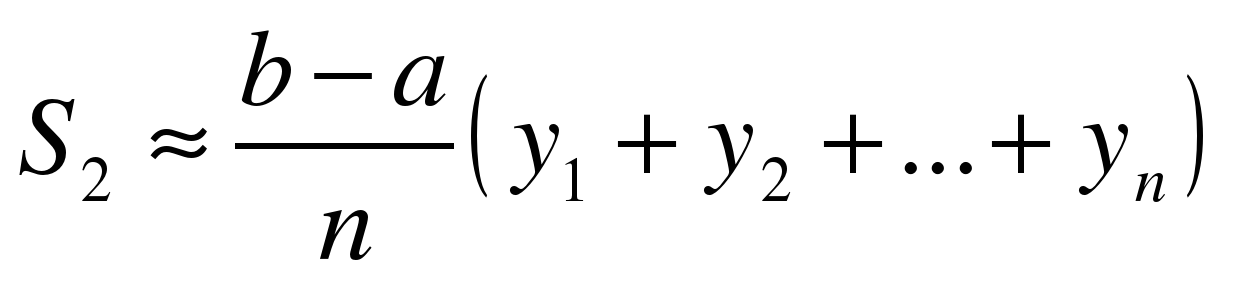 (2)
(2)
Эти формулы и называются формулами прямоугольников.
Для того, чтобы получить более точное значение определенного интеграла, необходимо найти среднее арифметическое площадей с недостатком (1) и с избытком (2).
Применение вычислительной техники значительно облегчит и убыстрит процесс вычисления по формулам прямоугольников, так как возможно выбрать минимально возможную величину шага – верхняя часть прямоугольников будет практически совпадать с линией криволинейной трапеции, причем значение шага можно менять. Вычисление значений функции в точках x0, x1,…,xn вычисляются циклически.
Пример: Найти 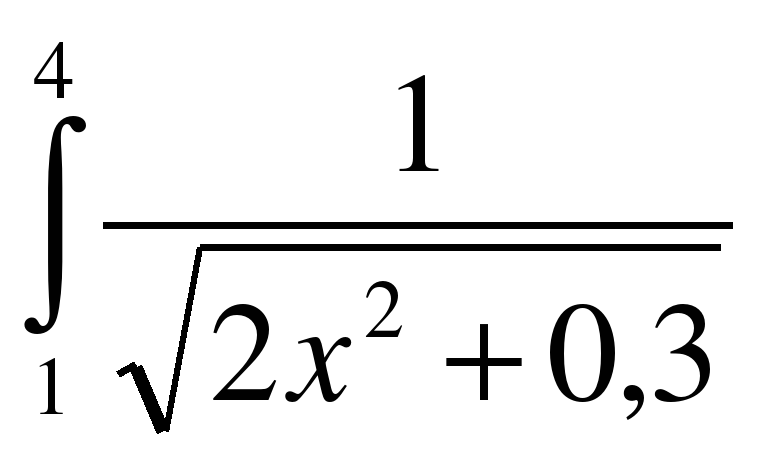
Предлагаемая программа вычисления:
Program PRIMOUGOLNIKI;
uses CRT;
Var {раздел описания переменных}
a,b,h,s1,s2,s,i:real;
Begin
ClrScr;
Writeln(‘введи значение нижнего предела интегрирования a’);
Readln(a);
Writeln(‘введи значение верхнего предела интегрирования b’);
Readln(b);
Writeln(‘введи значение шага h’);
Readln(h);
s1:=0; {находим площадь прямоугольников с недостатком}
i:=a;
While i
Begin
s1:=s1+(1/sqrt(2*i*i+0.3))*h;
i:=i+h;
End;
s2:=0; {находим площадь прямоугольников с избытком}
i:=a+h;
While i
Begin
s2:=s2+(1/sqrt(2*i*i+0.3))*h;
i:=i+h;
End;
s:=(s1+s2)/2;
Writeln(‘площади прямоугольников с недостатком и с избытком ’, s1:12:6,' ',s2:12:6);
Writeln(‘приближенное значение определенного интеграла’, s:12:6);
Readln;
End.
Правило трапеций
Оставим разбиение интервала [a, b] прежним, но заменим теперь каждую дугу линии 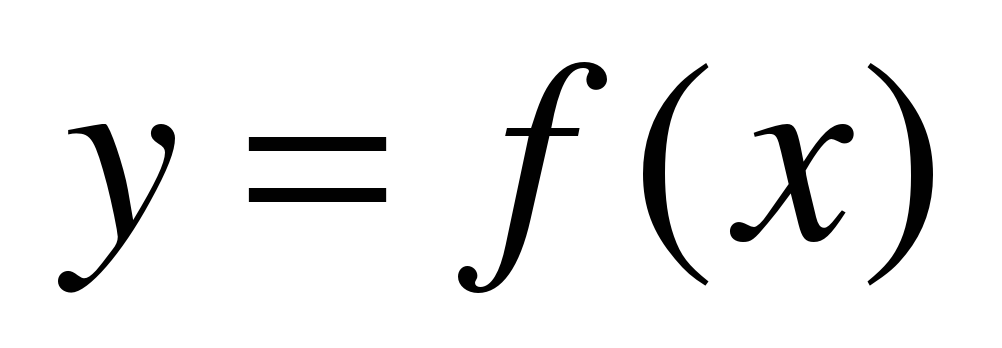 , соответствующую шагу, хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию n прямоугольными трапециями (рис. 3).
, соответствующую шагу, хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию n прямоугольными трапециями (рис. 3).
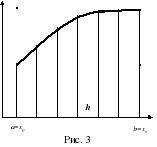
Геометрически очевидно, что площадь такой фигуры более точно выражает искомую площадь, чем площадь n-ступенчатой фигуры, составленной из прямоугольников.
Сумма площадей прямоугольных трапеций, построенных на величине h (шаге), равна:
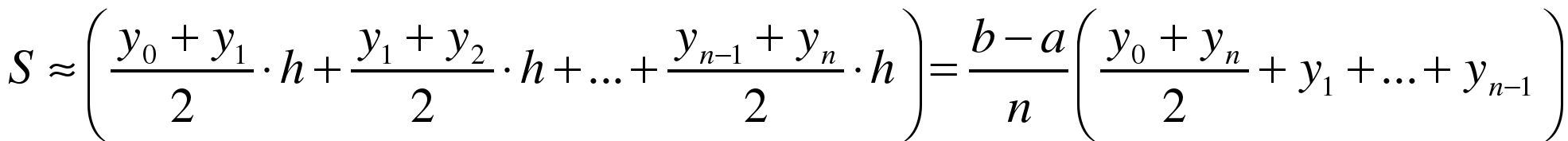 (3)
(3)
Эта формула и носит название формулы трапеций.
Если функция 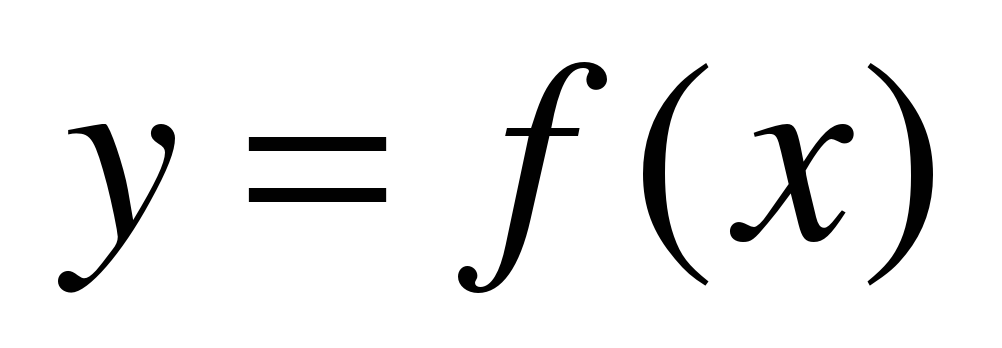 монотонна, то этот метод дает значение интеграла более точное, чем формулы прямоугольников.
монотонна, то этот метод дает значение интеграла более точное, чем формулы прямоугольников.
Убедимся в этом, составив программу вычисления того же интеграла.
Пример: Найти 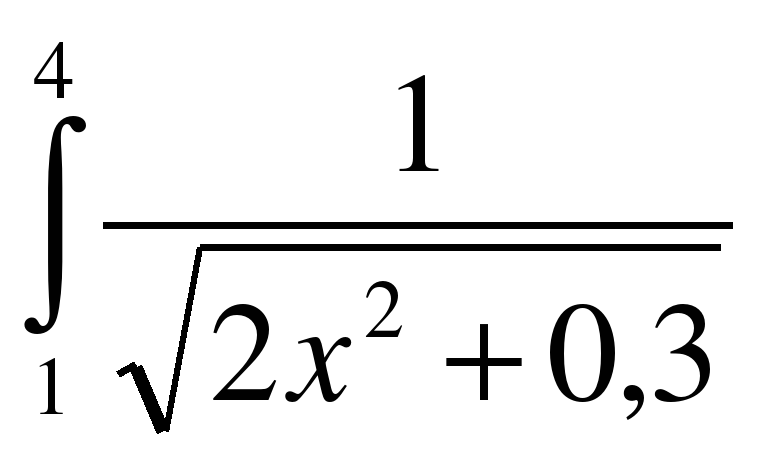
Program TRAPECII;
Uses CRT;
Var {раздел описания переменных}
a,b,h,s,i:real;
Begin
ClrScr;
Writeln(‘введи значение нижнего предела интегрирования a’);
Readln(a);
Writeln(‘введи значение верхнего предела интегрирования b’);
Readln(b);
Writeln(‘введи значение шага h’);
Readln(h);
s:=(1/sqrt(2*sqr(a)+0.3)+1/sqrt(2*sqr(b)+0.3))/2; {начальное значение суммы}
i:=a+h;
while i
begin
s:=s+1/sqrt(2*sqr(i)+0.3);
i:=i+h;
end;
s:=s*h;
Writeln(‘приблизительное значение определенного интеграла’, s:12:6);
Readln;
End.
Оценим полученные значения площадей, сравнив результаты вычислений, полученные при различном количестве разбиений, и убедимся, что при увеличении количества разбиений результат более точный.
| n | S |
| 100 | 31,14843731 |
| 10 000 | 31,79192345 |
| 1 000 000 | 31,79860977 |
В 11 классе после изучения темы «Определенный интеграл» вычислим точное значение площади следующим образом:
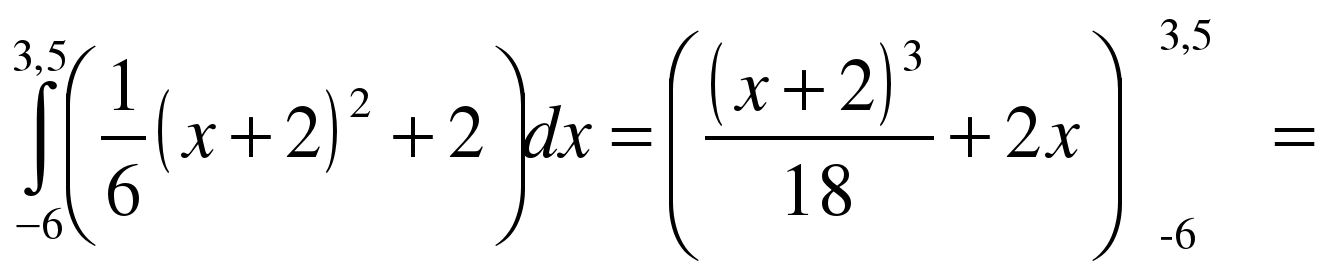

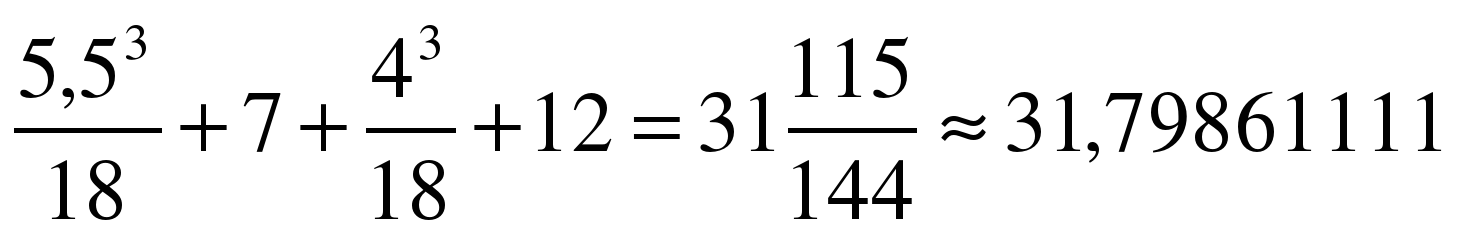
Интересно, что интегральное исчисление исторически возникло из необходимости решать задачи на определение площадей фигур и объемов тел. Корни этого метода уходят в III век до н.э.. Лучшие достижения древности в этой области принадлежат Архимеду. Приемы интегрального исчисления сейчас применяются в физике для вычисления работы, в экономике для вычисления объема произведенной продукции.
Самостоятельная работа по теме
Оцените результаты работы обеих программ с точки зрения точности и времени вычисления, произведя вычисления и заполнив таблицу:
| h | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| S1(с недостатком ) |
|
|
|
|
|
| S2 (с избытком) |
|
|
|
|
|
| S3 ( знач. опр. интеграла методом прямоугольников) |
|
|
|
|
|
| S( знач. опр. интеграла методом трапеций) |
|
|
|
|
|
Самостоятельно и по вариантам написать программы, отладить и вычислить значения интегралов двумя методами.
|
ВАРИАНТ № 1 1. 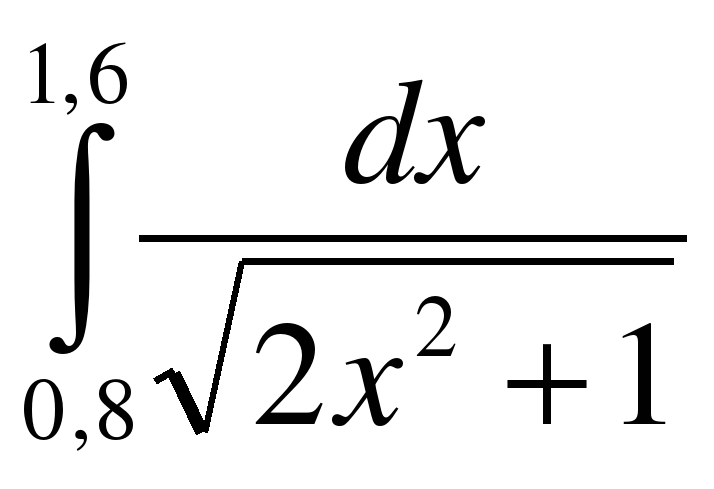
2. 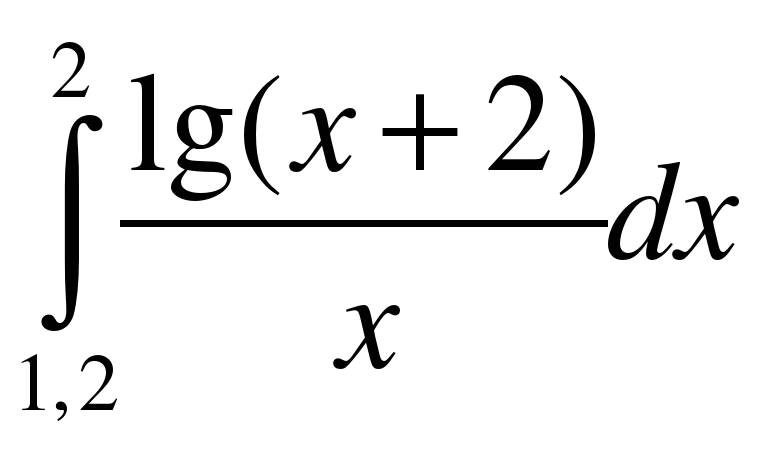
3. 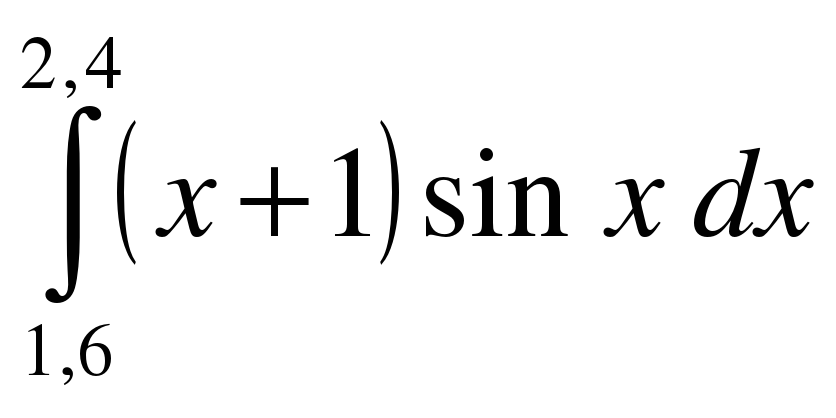
|
ВАРИАНТ № 2 1. 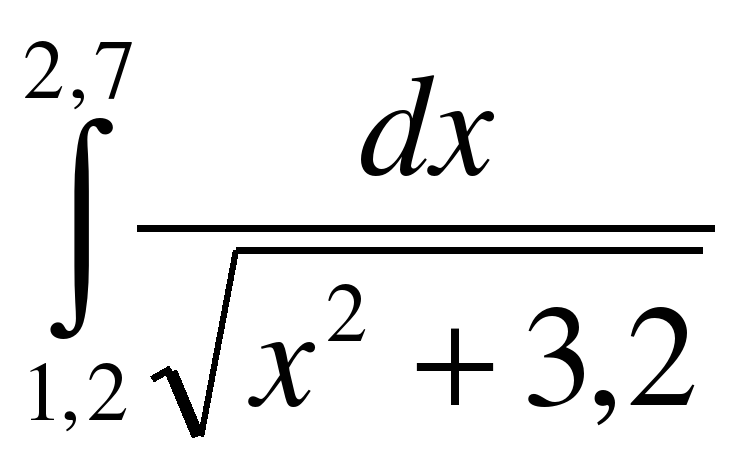
2.
3.
|
ВАРИАНТ № 3 1.
2.
3.
|
Заключение: Рассмотрев предложенную задачу, убедились, что данный метод позволяет с достаточной точностью рассчитать площадь криволинейной трапеции, основываясь на знании формул математики и основ программирования.

 Получите свидетельство
Получите свидетельство Вход
Вход






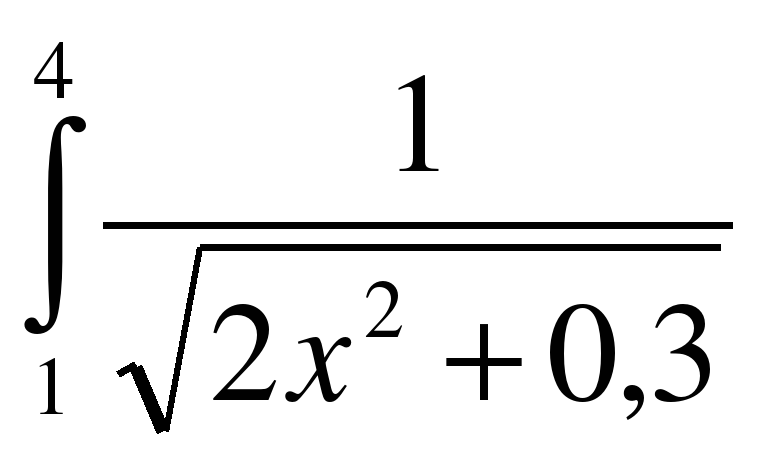

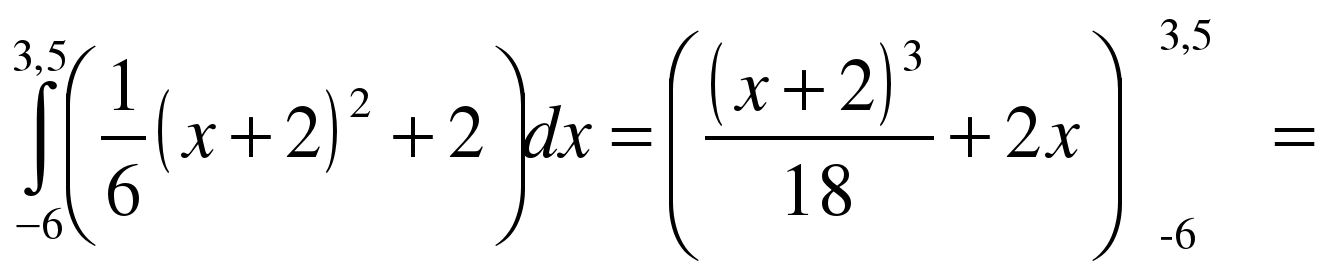

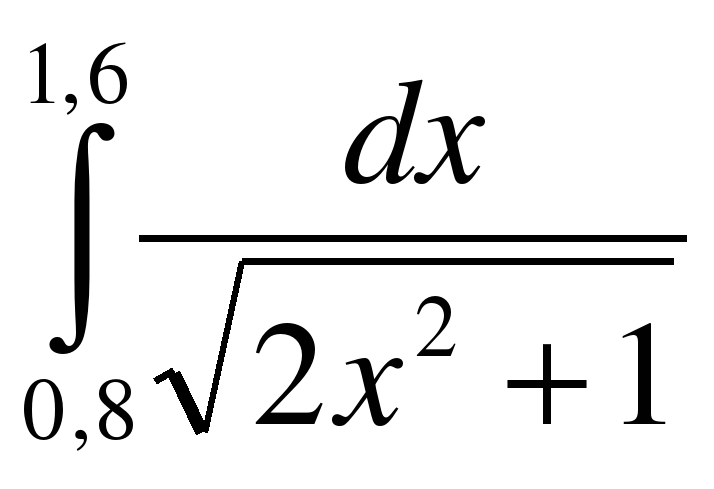
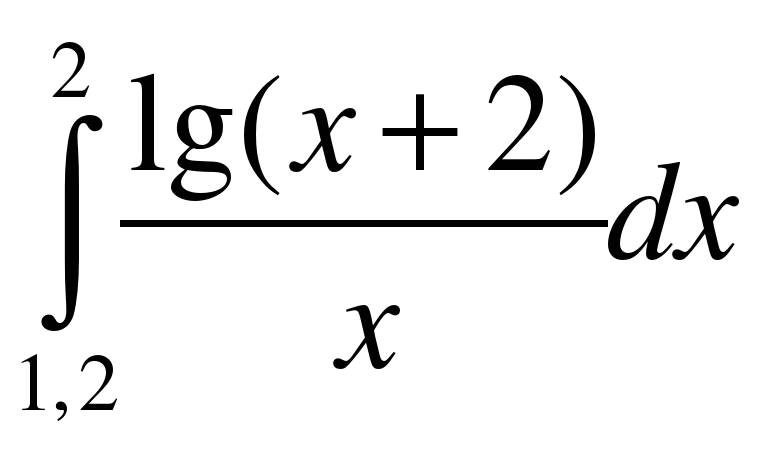
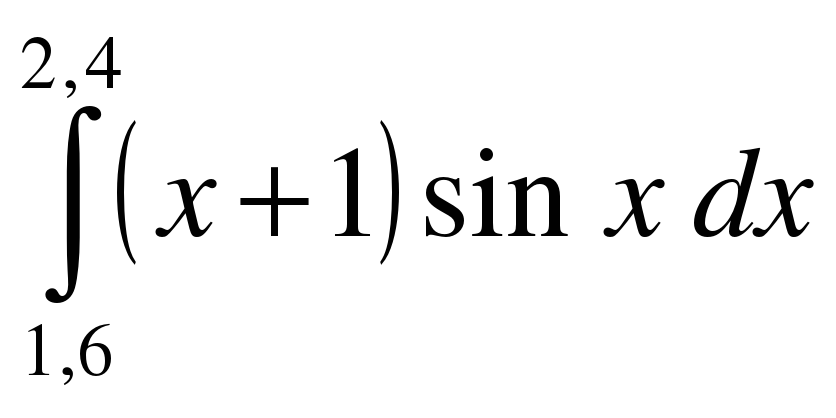
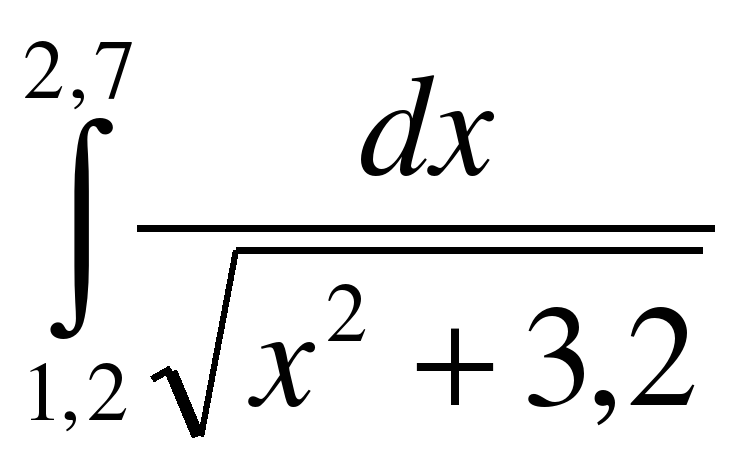









 Урок по математике и информатике "Численные методы математического программирования. Нахождение приближенного значения площади криволинейной трапеции" (0.1 MB)
Урок по математике и информатике "Численные методы математического программирования. Нахождение приближенного значения площади криволинейной трапеции" (0.1 MB)
 0
0 264
264 22
22 Нравится
0
Нравится
0


