Тема: «Решение уравнений и неравенств, содержащих несколько модулей»
Школа: Назарбаев Интеллектуальная школа физико – математического направления г. Астана
Учитель: Косова Галина Павловна, учитель математики
Цели и задачи урока: Показать преимущества метода интервалов как универсального метода решения задач с модулями. Обратить внимание на важнейшие свойства модулей, использование которых существенно упрощает решение задач.
Образовательная: Организовать деятельность учащихся по повторению свойств модулей. Рассмотреть приёмы и методы, ускоряющие решение некоторых классов задач с модулями.
Развивающая: Содействовать развитию исследовательских навыков, навыков анализа математической ситуации, умений символьной записи, устного счета, классифицировать многочлены.
Воспитательная: Содействовать развитию инициативности, трудолюбия, стремления к совершенствованию своих знаний.
Тип урока: комбинированный.
Форма проведения урока: лекция, беседа.
Структура урока:
Организация начала урока
Актуализация опорных знаний
Осознание и осмысление учебного материала.
Усвоение новых знаний
Первичная проверка понимания учащимися нового материала
Закрепление новых знаний
Задание на дом
Подведение итогов урока.
Рефлексия
Ход урока:
Тема: Решение уравнений и неравенств с несколькими модулями.
Имеются два основных пути решения уравнений с модулями. Первый путь- это раскрытие модулей в зависимости от знака выражений под модулем. Это универсальный способ, пригодный практически во всех случаях. Нельзя его применить только тогда, когда под модулем стоит настолько сложное выражение, что мы не можем исследовать его знак; например многочлен третьей степени, корни которого мы не можем пока найти.
Второй путь- использование следующего свойства модуля: уравнение 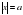 имеет решения
имеет решения 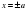 при
при 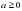 и не имеет решений при a
и не имеет решений при a
На первом уроке мы с вами отработали применение метода интервалов для построения графиков функций линейных, которые имеют несколько модулей. Этот метод существенно сокращает процедуру раскрытия модулей и делает решение задачи менее перегруженным.
Суть метода интервалов заключается в том, что если у подмодульных выражений найти нули, то между этими нулевыми точками выражения будут знакопостоянны. Это, в свою очередь, даст возможность на каждом из образовавшихся интервалов раскрыть модули и переписать исходное уравнение ( или неравенство) уже в обычной форме. Решив его, в ответ надо включить только те решения, которые этому промежутку принадлежат.
Удобно решение уравнения (неравенства)непосредственно вести под тем интервалом, в котором раскрывались модули, тем самым как бы постоянно напоминая себе в какой области происходит решение.
Рассмотрим пример: Решить уравнение 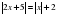
Решение: Действуем так же, как при построении графика. Отметим на числовой прямой точки, в которых выражения под модулем обращается в ноль: 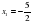 ,
, 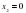 . На каждом из полученных интервалов выражения под мордулем имеют один знак, и мы его определим.
. На каждом из полученных интервалов выражения под мордулем имеют один знак, и мы его определим.

Третья система решений не имеет, поскольку решение уравнения, входящего в систему, не удовлетворяет неравенству системы. Ответ: -1; -7.
Рассмотрим второй пример: 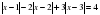
Решение: Выражения под модулем обращаются в норль в трёх точках: 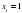 ,
,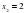
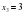 ,
,
И мы получим на числовой прямой четыре интервала.
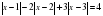
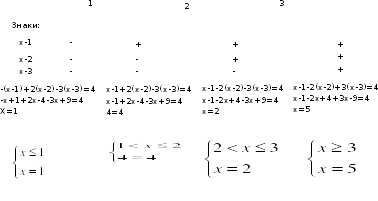
Первая система имеет решение x=1, решение второй системы все числа интервала (1;2] и в третьей системе ответ x=5. Объединяя решения всех систем, получим множество x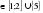 .
.
Проверим графически полученное решение. Для этого рассмотрим график функции 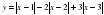 (он был построен на первом уроке). Проведём горизонтальную прямую y=4 и найдём точки пересечения. Абсциссы этих точек и будут решениями уравнения.
(он был построен на первом уроке). Проведём горизонтальную прямую y=4 и найдём точки пересечения. Абсциссы этих точек и будут решениями уравнения.
Ответ: 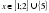
![]()
![]()
![]()
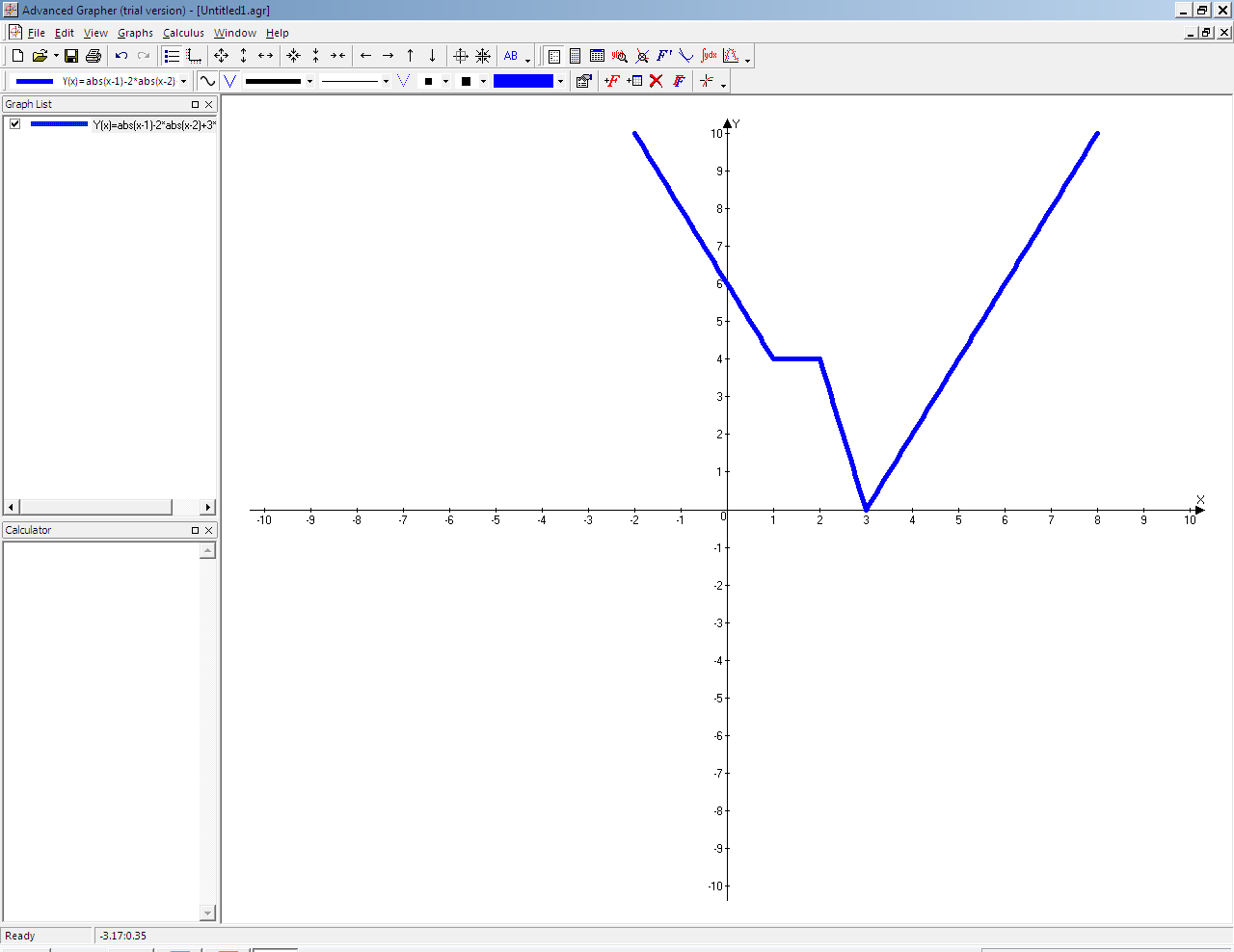
Y=4
Пример 3. 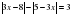
Решение. Заметим, что выражение 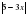 лучше сразу переписать в виде
лучше сразу переписать в виде 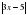 . На основании свойства, рассмотренного на первом уроке
. На основании свойства, рассмотренного на первом уроке 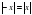 , ( очевидно это одно и тоже). Итак, решаем уравнение
, ( очевидно это одно и тоже). Итак, решаем уравнение 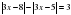 . Находим точки, в которых выражения под модулеми обращается в ноль:
. Находим точки, в которых выражения под модулеми обращается в ноль:  ,
,  .
.

Первой системе удовлетворяют все точки при 
Вторая система имеет решение x=  , а третья система не имеет решения, так как содержит неверное неравенство. Ответ:
, а третья система не имеет решения, так как содержит неверное неравенство. Ответ: 
Метод интервалов при решении неравенств.
При решении неравенств аналогично работает метод интервалов.
Чтобы не сделать ошибки, не нарушить знакопостоянство на интервалах между нулями, необходимо помнить, что у каждого подмодульного выражения коэффициент при x должен быть положительным. Это сделать легко, если помнить свойство модуля:  или
или 
Решить неравенство: 


Используем опять метод интервалов. Нули подмодульных выражений:  ,
, 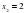 ,
, 
x
Объединяем все ответы: 
На вступительных экзаменах в МГУ, 1995г. был такой пример:
Найти все значения параметра а, при которых уравнение 
Имеет ровно два корня.
Эту задачу, конечно, можно решить впрямую, т.е. при всех значениях а, выбрав в конце все нужные значения параметра. Но это довольно долго. И опять нас выручит метод интервалов и графическая иллюстрация. Уравнение вида f(x)=a равносильно системе  , решение которой, в свою очередь, графически представляет из себя нахождение точек пересечения функции y=f(x) и прямой y=a. Это решение можно получить, если мы чётко понимаем, как выглядит график функции y=f(x).
, решение которой, в свою очередь, графически представляет из себя нахождение точек пересечения функции y=f(x) и прямой y=a. Это решение можно получить, если мы чётко понимаем, как выглядит график функции y=f(x).
Перепишем исходное уравнение в виде  . В котором переменные «разделены»: слева функция только от x, справа-константа, зависящая от а.
. В котором переменные «разделены»: слева функция только от x, справа-константа, зависящая от а.
В основе построения этого графика всё тот же метод интервалов, так хорошо уже изученный нами.
Чтобы завершить решение задачи, необходимо мысленно прямую y=2 , параллельную оси абсцисс, и передвигая её вдоль оси ординат, выяснить, при каких значениях 2
, параллельную оси абсцисс, и передвигая её вдоль оси ординат, выяснить, при каких значениях 2 эта прямая пересекает построенный график ровно в двух точках. Понятно, что это возможно либо когда
эта прямая пересекает построенный график ровно в двух точках. Понятно, что это возможно либо когда
 , либо когда 2
, либо когда 2 =10.
=10.
Ответ: (0;3) 
![]()
y=2
Важнейшие свойства модулей, использование которых существенно упрощает решение задач
Для начала перечислим основные свойства модулей. Часть из них являются наиболее употребляемыми, вывод их несложен, а удобство значительно, поэтому лучше всего их всегда держать в «оперативной памяти».
1. 2.
2.  3.
3.  4.
4. 
 5.
5. 

6.  7.
7.  8.
8.  9.
9. 
Если заранее быть готовыми к встрече с ними, скорость решения может существенно возрасти.
Пример №1.
Решить уравнение: 
Понятно, что свойство 2 превращает это равенство в тождество, получается 0=0. Остаётся только учесть ограничение  Ответ:
Ответ: 
Пример №2 Решить неравенство: 
Последовательное применение свойств 6 и 5. Сразу же даёт ответ.
Ответ: 
Приёмы и методы, ускоряющие процесс решения некоторых задач с модулями
Есть задачи, которые можно и нужно решать быстрее, чем это позволяет метод интервалов ( промежутков). Первые среди них – это простейшие уравнения и неравенства с одним модулем, решением которых заканчиваются практически каждая более-менее сложная задача. Например,  ;
;  ;
;  ; или
; или 
Их решения может быть достаточно быстро получено из геометрической интерпретации модуля. Ведь известно, что геометрически модуль представляет собой расстояние между двумя точками.
Например,  - есть расстояние между точкой x на координатной прямой и точкой 3 этой прямой. Поэтому для решения
- есть расстояние между точкой x на координатной прямой и точкой 3 этой прямой. Поэтому для решения  достаточно выяснить, где расположены все точки прямой, отстоящие от точки 3 на расстоянии 2. Понятно, что это точки x=1, x=5/.
достаточно выяснить, где расположены все точки прямой, отстоящие от точки 3 на расстоянии 2. Понятно, что это точки x=1, x=5/.
Точно также для решения неравенства  надо определить все точки числовой прямой, расстояние от каждой из которых до точки 3 больше 1.- это множество
надо определить все точки числовой прямой, расстояние от каждой из которых до точки 3 больше 1.- это множество  .
.
Решая неравенство  , ищем точки числовой прямой, расстояние от которых до точки 3 не больше 5, т.е. множество
, ищем точки числовой прямой, расстояние от которых до точки 3 не больше 5, т.е. множество  . Что касается неравенства
. Что касается неравенства  , то его решением, очевидно, является пересечение этих двух множеств. Удобно всё это изобразить на рисунке:
, то его решением, очевидно, является пересечение этих двух множеств. Удобно всё это изобразить на рисунке:
![]()
![]()
![]()
![]()


Более сложные задачи по пройденному материалу
Большое количество «вложенных» друг в друга модулей всегда настораживает. Сложность следующей задачи больше психологическая. Однако правила раскрытия модулей на интервалах исследования спокойно работают, практически не требуя от нас новых приёмов. Единственный совет: если раскрывать «вложенные» модули по этим правилам, то удобнее начинать это делать с внутреннего модуля.
Решить уравнение: 
Рассматриваем два случая.
А) x

 или
или
или 

Б) x
В этом случае 






 x
x
Ответ:  ;
; .
.
Например: 
Однако в этой задаче надо заметить, что внешний модуль легко снимается, т.к. под ним стоит положительная функция, а потому неравенство становится уже более-менее «обычным».















3
1
7
-3
![]()
![]()
![]()

![]()
![]()



![]()

![]()
![]()
![]()
Ответ: x (-3;1)
(-3;1)  (3;7)
(3;7)
Рассмотрим другой пример: 
Каких- то упрощений в этой задаче уже не видно. Понятно, что, используя метод интервалов, мы будем вынуждены рассматривать достаточно много случаев, попробуем действовать иначе.











Ответ:x (-
(-
В задачах для самостоятельного решения будет ещё немало примеров, которые, несмотря на внешнюю сложность, решаются изученными нами методами.
Задачи для самостоятельного решения:
1.
2.
3.
4.
5. 
Теоретические факты, которые мы разобрали на этом уроке вы найдёте на сайте:
http://uztest.ru/abstracts/?idabstract=95

 Получите свидетельство
Получите свидетельство Вход
Вход



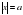 имеет решения
имеет решения 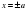 при
при 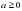 и не имеет решений при a
и не имеет решений при a 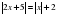
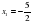 ,
, 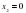 . На каждом из полученных интервалов выражения под мордулем имеют один знак, и мы его определим.
. На каждом из полученных интервалов выражения под мордулем имеют один знак, и мы его определим.
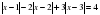
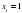 ,
,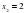
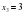 ,
,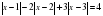
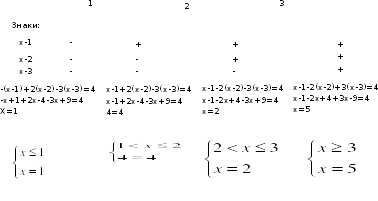
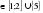 .
.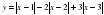 (он был построен на первом уроке). Проведём горизонтальную прямую y=4 и найдём точки пересечения. Абсциссы этих точек и будут решениями уравнения.
(он был построен на первом уроке). Проведём горизонтальную прямую y=4 и найдём точки пересечения. Абсциссы этих точек и будут решениями уравнения. 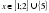

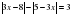
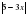 лучше сразу переписать в виде
лучше сразу переписать в виде 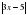 . На основании свойства, рассмотренного на первом уроке
. На основании свойства, рассмотренного на первом уроке 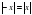 , ( очевидно это одно и тоже). Итак, решаем уравнение
, ( очевидно это одно и тоже). Итак, решаем уравнение 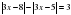 . Находим точки, в которых выражения под модулеми обращается в ноль:
. Находим точки, в которых выражения под модулеми обращается в ноль: 








 Конспект урока математики "Решение уравнений и неравенств с несколькими модулями" (0.36 MB)
Конспект урока математики "Решение уравнений и неравенств с несколькими модулями" (0.36 MB)
 0
0 1268
1268 100
100 Нравится
0
Нравится
0


