Оглавление
Введение………………………………………………………………………3
§1 Графы Кэли………………………………………………………………...4
§2 Структура группы А
……………………………………………………..6
§3 Классификация порождающих подмножеств типа (2,3) и (2,5)……….8
§4 Графы Кэли, соответствующие найденным порождающим множествам………………………………………………………………………...9
Список литературы………………………………………………………….18
Введение
Графы Кэли являются предметом активного изучения в последние 40 лет. При этом в центре внимания находятся проблемы изоморфизма и существования гамильтоновых циклов. Еще в 1959 году была высказана гипотеза о том, что все конечные графы Кэли порядка 2 гамильтоновы. Эта гипотеза была доказана только для абелевых групп и для метабелевых групп с примарным циклическим коммутантом. С другой стороны, в последнее время возник большой интерес к графам Кэли простых конечных групп и симметрических групп, поскольку эти графы широко применяются в качестве моделей коммуникационных сетей. Наименьшей простой некоммутативной группой является знакопеременная группа A5, т.е. группа всех четных перестановок степени 5. До сих пор неизвестно, является ли любой граф Кэли этой группы гамильтоновым. Очевидно, для ответа на этот вопрос достаточно исследовать все графы Кэли, соответствующие минимальным порождающим множествам.
В работе изучаются кубические графы Кэли группы A5 для случаев, когда порождающее множество имеет вид {a, b, b-1}, где a – элемент порядка 2 и b – элемент порядка 3 или 5. Проведена классификация таких порождающих множеств с точностью до изоморфизма (т.е. до сопряженности в симметрической группе). Показано, что этим порождающим множествам соответствуют три неизоморфных графа Кэли. Для каждого из этих графов построен гамильтонов цикл. Кроме того, найдены диаметры этих графов и показано, что два из них планарны, а третий не планарен.
§1 Графы Кэли
Пусть G – группа и А – подмножество G, замкнутое относительно взятия обратного элемента и не содержащее нейтрального элемента. Тогда графом Кэли называется граф C(G, A), вершинами которого являются элементы группы G, а ребра имеют вид {x, xa}, где a принадлежит подмножеству А[1].
Любой граф Кэли регулярен: степень каждой вершины равна мощности множества А.
Граф Кэли C(G, A) является связным если и только если множество А порождает группу G т. е. каждый элемент из G представляется в виде произведения элементов из А. В дальнейшем мы будем рассматривать только связные графы Кэли[2].
Граф называется гамильтоновым, если он содержит гамильтонов цикл, т.е. простой цикл, проходящий через все вершины. Имеется гипотеза о том, что любой граф Кэли порядка 2 гамильтонов [3]. Эта гипотеза доказана только для абелевых групп и для некоторых классов групп, близких к абелевым. Для простых конечных групп (в частности, для знакопеременных групп An при n 5) вопрос остается открытым.
Для каждой группы можно построить много графов Кэли. Естественен вопрос: когда графы Кэли одной группы, соответствующие различным порождающим множествам, изоморфны?
Два порождающих множества А и В группы G называются изоморфными, если существует автоморфизм 
группы G такой, что (А)=В. Изоморфным порождающим множествам соответствует изоморфные графы Кэли. Действительно, если x и y – смежные вершины C(G, A), то y=xa для некоторого а
А, и тогда φ(у)=φ(х)φ(а), где φ(а)В т.е. φ(х) и φ(у) – смежные вершины C(G, A)[1].
Обратное утверждение не верно. Два графа Кэли группы G могут быть изоморфны, даже если их порождающие множества неизоморфны. Тем не менее, в большинстве случаев неизоморфным порождающим множествам соответствуют неизоморфные графы Кэли[3].
В работе рассматриваются графы Кэли группы A5 для случая, когда порождающее множество имеет вид {a, b, b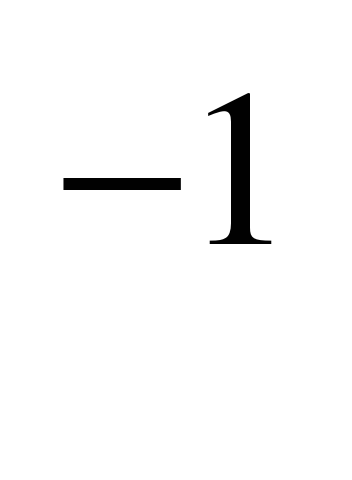
}, где а – инволюция (т.е. элемент порядка 2) и b – элемент порядка 3 или 5. В следующем параграфе дается классификация всех таких порождающих множеств с точностью до изоморфизма.
§2 Структура группы А
Через А обозначается знакопеременная группа степени 5, т.е. группа всех четных перестановок элементов 1,2,3,4,5. Это группа порядка 60, которая является наименьшей некоммутативной простой группой. Группа А содержит, кроме 1, элементы порядков 2, 3 и 5, а именно, 15 элементов циклического типа (ab)(cd), 20 циклов (abc) длины 3 и 24 цикла (abcxy) длины 5.
Через S обозначается симметрическая группа степени 5. Любой автоморфизм группы А индуцируется внутренним автоморфизмом группы S. А является ее нормальной подгруппой индекса 2.
При этом два элемента группы А сопряжены в S тогда и только тогда, когда они имеют одинаковый циклический тип, т.е. содержат одинаковое число циклов каждой длины.
При классификации порождающих множеств в А использована информация о максимальных подгруппах. Очевидно, два элемента а, b порождают группу А если и только если они не входят не в одну из ее максимальных подгрупп[1].
Группа А содержит 5 максимальных подгрупп порядка 12. Каждая из них является стабилизатором одного из элементов 1…5 т.е. состоит из всех перестановок, оставляющий данный элемент неподвижным.
Пусть а – инволюция. Очевидно, элементы а и b входят в максимальную подгруппу порядка 12 тогда и только тогда, когда b – элемент порядка 3 и при этом а и b имеют общую неподвижную точку.
Кроме того А содержит 6 максимальных подгрупп порядка 10, каждая из которых изоморфна диэдральной группе D т.е. группе симметрий правильного пятиугольника с вершинами 1,2,3,4,5. Если b – цикл длины 5, то элементы а и b входят в такую подгруппу тогда и только тогда, когда ab – инволюция.
Также в группе А имеется 10 максимальных подгрупп порядка 6, которые являются стабилизаторами двухэлементных подмножеств
Типом порождающего множества будем называть набор порядков его элементов.
§3 Классификация порождающих подмножеств типа (2,3) и (2,5)
Пусть а – инволюция и b – цикл длины 3. Так как все инволюции в группе A5 сопряжены, то можно считать, что a = (12)(34). Элементы а и b порождают группу А тогда и только тогда, когда тройной цикл содержит неподвижную точку 5 инволюции a и по одному элементу из каждой транспозиции. Получим 4 таких тройных цикла, все они сопряжены относительно стабилизатора инволюции а, поэтому в качестве элемента b можем взять (135). Таким образом, множество: B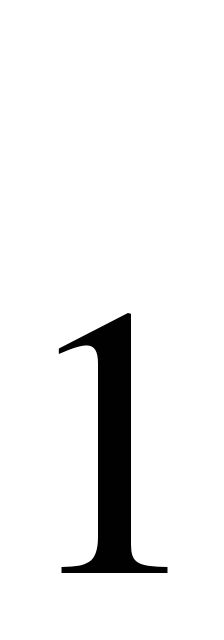
={(12)(34), (135), (315)} является единственным с точностью до изоморфизма симметричным порождающим множеством типа (2,3).
Зафиксируем b=(12345) и рассмотрим циклическую подгруппу, порожденную этим элементом. Эта группа действует транзитивно на множестве (12345) и содержится в централизаторе элемента b. Поэтому сопряжение некоторым элементом этой подгруппы переводит a в одну из трех инволюций с неподвижной точкой 5: (12)(34), (13)(24), (14)(23). Вместе с b в диэдральную подгруппу входит перестановка (14)(23), а две другие образуют два неизоморфных порождающих множества.
§4 Графы Кэли, соответствующие найденным порождающим множествам
Граф Кэли группы А с порождающим множеством {(12)(34), (135), (315)} изоморфен усеченному додекаэдру.
Рисунок 1. Усеченный додекаэдр
Основные характеристики:
Рисунок 2. Гамильтонов цикл
Граф с порождающим множеством {(12)(34), (12345), (15432)} изоморфен усеченному икосаэдру.
Рисунок 3 Усеченный икосаэдр
Основные характеристики графа:
Рисунок 4 Гамильтонов цикл
Граф с порождающим множеством {(13)(24), (12345), (15432)}:
Рисунок 5 Сау(А, {(13)(24), (12345), (15432)})
Основные характеристики:
число вершин равно 60;
число ребер 90;
степень каждой из вершин равна 3;
хроматическое число равно 3;
d=6;
не планарен (содержит К в качестве подграфа)
гамильтонов (Рис. 6)
Рисунок 6 Гамильтонов цикл
Если сравнить полученные результаты, то можно сделать вывод о том, что полученные графы неизоморфны. Например, у них разные диаметры.
Список литературы
1. S.J.Currar, J.A.Galian, Hamiltonion cycles and paths in Cayley graphs and digraphs a survey, Discrete Math. 156(1996), 1 – 18.
2. E.Rapaport – Strasser, Cayley color groups and Hamilton line, Scripta Math. 24(1959), 51 – 58.
3. I.Park, R.Padoicic, Hamiltonion paths in Cayley graphs, preprint
18
Получите свидетельство
Вход
Графы Кэли группы А5 для порождающих множеств типа (2, 3) и (2, 5) (0.15 MB)
0
763
56
Нравится
0
