ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики
Либерман А.М.
Разработка системы итогового повторения курса алгебры 7-9-х классов.
Примерное планирование.
Ноябрь. Работа №1
Декабрь. Работа №2
Январь. Работа №3
Февраль. Работа №4
Март. Работа №5
Апрель. Работа №6
Май. Итоговая работа №7
Оглавление
Работа №1. «Числа и вычисления» 2
Работа №2. «Алгебраические выражения» 3
Работа №3. «Уравнения. Системы уравнений» 4
Работа № 4. «Неравенства. Системы неравенств» 5
Работа №5. «Последовательности и прогрессии» 6
Работа № 6. «Функции» 7
Работа №7. Итоговое повторение. 8
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа №1. «Числа и вычисления»
Среди значений выражений 30; 3-1; 3-2; 3-3 укажите наибольшее:
30 2) 3-1 3) 3 -2 4) 3-3
Диаметр планеты Юпитер приближенно равен 142600км. Как эта величина записывается в стандартном виде?
1,426 · 104 км 2) 1,426 · 102 км 3) 14,26 · 104 км 4) 1,426 · 105 км
Какое из указанных чисел является значением выражения 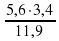 ?
?
0,16 2) 1,6 3) 16 4) 160
Значение выражения 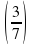 -2 равно
-2 равно
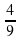 2) –
2) – 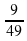 3) –
3) – 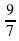 4)
4) 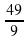
Во сколько раз число 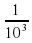 меньше числа
меньше числа 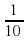 ?
?
10 2) 1000 3) 0,1 4) 2
Товар уценили на 20%, при этом он стал стоить 680р. Сколько стоил товар до уценки?
136 р 2) 816 р 3) 700 р 4) 850 р
Ответ. ________________________
Вычислите: 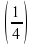 -2 – 4-3 : 4-5 + 20120
-2 – 4-3 : 4-5 + 20120
Ответ. ___________________
Соотнесите выражения с их значениями
А. 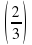 2 Б.
2 Б. 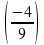 -1 В.
-1 В. 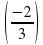 -2
-2
1) 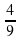 2)
2) 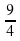 3)
3) 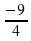
Найдите значение выражения 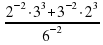 .
.
Ответ. _____________________
Сравните выражения а= 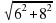 и b = 6+8
и b = 6+8
Ответ. _____________________
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа №2. «Алгебраические выражения»
Упростите выражение 4(m – 1)2 + 8m
4m2 + 8m + 4 2) 4m2 + 8m – 4 3) 4m2 + 4 4) 4m2 +1
Найдите значение выражения 1 –5k + 20k2 при k = – 0,2
Ответ.______________________
Из формулы кинетической энергии Ек = 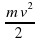 выразите m.
выразите m.
m = 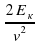 2) m =
2) m = 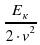 3) m =
3) m = 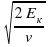 4) m =
4) m = 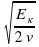
В каком случае выражение преобразовано в тождественно равное?
(y + x)(x – y) = x2 – y2 3) x2 + 2xy + y2 = (x + y)2
5(x + 2y) = 5x + 2y 4) 4 – x2 = (2 – x)2
Какое из выражений не имеет смысла при х = 2 и х = 3?
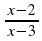 2)
2) 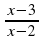 3)
3) 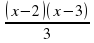 4)
4) 
Преобразуйте в многочлен выражение 6p(p – 2) – (p – 6)2.
Ответ.________________________
Сократите дробь  .
.
a2 – 3ab + 9b2 3) a2 – 3ab + b2
a2 + 3ab + 9b2 4) a2 + 6ab + b2
Разложите на множители квадратный трехчлен 3х2 + 2х – 1.
(3х – 1)(х + 1) 3) (х –  )(х + 1)
)(х + 1)
(х +  )(х – 1) 4) (3х + 1)(х – 1)
)(х – 1) 4) (3х + 1)(х – 1)
Найдите разность выражений  – 3х.
– 3х.
Ответ. ________________________
10 м упаковочной бумаги стоят a рублей. Составьте выражение для вычисления стоимости n см бумаги (в рублях).
10000an 2)  3)
3)  4)
4) 
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа №3. «Уравнения. Системы уравнений»
Решите уравнение 7х – 6 = (2х + 3) · 2
Ответ. ______________________
Какое из чисел является корнем уравнения х3 – 6х2 + 13х – 20 = 0?
– 1 2) 0 3) 1 4) 4
Какое из предложенных уравнений имеет два различных корня?
х2 + 5х – 21 = 0 3) 2х2 – 3х + 1 = 0
9х2 + 6х +1 = 0 4) 3х2 + 2х – 2 = 0
Каждое уравнение соотнесите со множеством его корней.
А) z2 – 16 = 0 Б) z2 + 4z = 0 В)  = 0
= 0
1) 0 и – 4 2) 0; 4, 16 3) – 4 и 4 4) 0 и 4
Один из корней уравнения х2 + pх – 15 = 0 равен 5. Найдите сумму его корней.
Ответ. _____________________
Не решая уравнения 3х2 + 3х – 1 = 0, найдите х12 х2 + х1 х22,
где х1 и х2 – корни уравнения.
Ответ. _______________________
Вычислите координаты точки пересечения прямых 6х + 5у = –1, 7х – 3у = –10.
Ответ. _________________________

Из данных уравнений подберите второе уравнение системы х2 + у2 = 16 так, чтобы
……………
она не имела решений.
у = х 2) х = 4 3) у = - 4 4) х = 16

Решите систему уравнений х3 + у3 = 7,
х2у + ху2 = – 2 .
Ответ. ________________________

При каком а система уравнений 3х + 4у = - 19,
2х – 5у = 18,
х + у – а = 5.
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа № 4. «Неравенства. Системы неравенств»
Число 5 является решением неравенства
(2х – 10)2 х2 – 26 3) (2х – 10)2 х2 + 25
х2 2х – 10 4) х2 – 50 (х – 5)2
При каких значениях х имеет смысл выражение  ?
?
х ≠ 6 2) х 6 3) х - 6 4) х 6
Решите неравенство: 4х2 + 4х + 1 0
Ответ. ______________________
Если a b, то для любых a и b верно неравенство
– 5a – 5b 3) a2 b2
2 – a 2 – b 4) a + 4 b + 4
Решите двойное неравенство – 30 ≤ 3 – 11у ≤ – 8
Ответ. _______________________________

На координатной прямой отмечены числа a, b, c . . . .
a 0 b c
Из следующих утверждений выберите верное.
ac 0 2) b – a 0 3) c – b 0 4) c – a 0
Решите неравенство  (х – 4) + 1 ≤
(х – 4) + 1 ≤  х
х
х ≤ –  2) х
2) х  –
– 3) х ≤ – 5 4) х ≤ 5
3) х ≤ – 5 4) х ≤ 5

Решите систему неравенств 5х – 2 ≥ – 12,
0,5 х 4
Ответ. ______________________
Найдите область определения выражения 
Ответ. _________________________

Укажите наименьшее целое решение системы неравенств
5х – 4(2х – 1) 3 (х + 2),
9 – х2 ≥ 0
Ответ. ______________________
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа №5. «Последовательности и прогрессии»
Найдите девятый член арифметической прогрессии 3; 7; …
33 2) 34 3) 35 4) 36
Какое число не является членом арифметической прогрессии: 5; 8; 11; …..?
53; 2) 62; 3) 82 4) 95
Каждой последовательности, заданной формулой n – ного члена, поставьте в соответствие верное утверждение,
А. аn = 3n2 Б. bn = 3n B. сn = 3n
1) последовательность – арифметическая прогрессия;
2) последовательность – геометрическая прогрессия;
3) последовательность не является прогрессией.
Найдите четвертый член арифметической прогрессии (an), если а3 + а5 = 24.
9 2) 10 3) 15 4) 21
Геометрическая прогрессия (bn) задана условиями: b1 = 3, bn+1 = bn · 2. Укажите формулу n – го члена этой прогрессии.
bn = 3 · 2n + 1 2) bn = 3 · 2n 3) bn = 3 · 2n 4) bn = 3 · 2(n – 1)
Поезд за первую минуту прошел 200 м. За каждую следующую минуту поезд проходил на 100 м больше, чем в предыдущую. Какое расстояние (в метрах) прошел поезд за
n –ую минуту?
100n + 200 2) 200n + 200 3) 100n + 100 4) 200n + 200
Последовательность an задана формулой an = n2 – 2n – 1. Найдите номер члена последовательности, равного 7.
Ответ. ________________________
Найдите сумму отрицательных членов арифметической прогрессии: –10; – 9,8; ….
Ответ. __________________________
Для каждой арифметической прогрессии, заданной двумя членами, укажите её разность d.
А. а2 = 3, а3 =2 Б. а4 = 7, а7 = 1 В. а1 = 4, а5 = 8
1) d = 1 2) d = – 1 3) d = –2 4) d = 2
Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 110.
Ответ. ________________________________
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа № 6. «Функции»
Постройте график функции у = 13 – 2х2 + 10х. Укажите наибольшее значение функции.
Ответ.________________________


По графику линейной функции у = kx +m y
определите знаки коэффициентов k и b.

k b 0 3) k 0, b 0 x
k 0, b 0 4) k 0, b 0
Укажите точку, которая принадлежит графику функции у =  .
.
А(0; 5) 2) В(1; 0,5) 3) С( 2; 10) 4) D(–1; 2)
Установите соответствие между функциями и их графиками. Функции заданы формулами:
А. у =  Б. у = –4х2 – х В. у = –4х – 1
Б. у = –4х2 – х В. у = –4х – 1
1) парабола 2) прямая 3) гипербола
Графики функций у = 5х – 7 и у = 2х – 1 пересекаются в точке
(2; 3) 2) ( –2; 3) 3) (3; –2) 4) (–3; –2)
Найдите уравнение прямой, параллельной прямой у = –3х + 7 и проходящей через точку М (2; 2)
Ответ. ___________________
Парабола с вершиной в точке (1; 2) проходит через точку с координатами (–2; –1). В каких точках парабола пересекает ось абсцисс?
Ответ. __________________________
Проходят ли через одну точку прямые у = 8 – 2х, у = 2х, у = 3х – 2?
Ответ. __________________________
Прямая х = 1 – ось симметрии параболы у = ах2 + (а2 – 8)х + 2, ветви которой направлены вверх. Найдите координаты вершины параболы.
Ответ. __________________________
Прямая у = – 9х пересекает параболу у = х2 – 10 в двух точках. Выясните координаты точки, которая располагается ниже оси абсцисс.
Ответ. ___________________________
ГБОУ СОШ № 654 имени А.Д. Фридмана
учитель математики Либерман А.М.
Работа №7. Итоговое повторение.
Расположите в порядке убывания числа 0,45; 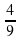 ; 0,405.
; 0,405.
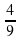 ; 0,45; 0, 405 3)
; 0,45; 0, 405 3) 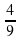 ; 0,405; 0, 45
; 0,405; 0, 45
0,45; 0,405; 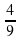 4) 0,45;
4) 0,45; 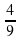 ; 0,405
; 0,405
Упростите выражение 2 –
–  +
+  .
.
0 2) 3 3) 5
3) 5 +
+  4)
4)  –
–
Цена товара повысилась на 40%. Сколько рублей стоит товар, если его первоначальная стоимость 320 рублей?
128 2) 800 3) 448 4) 1320
Решите неравенство 3(х – 5)(х + 4) ≤ 0
Ответ. ______________________
Маленькая коробка карандашей стоит а рублей, а большая коробка стоит b рублей. Сколько рублей заплатили за 15 маленьких коробок и p больших?
15а + bp 2) 15(a + b + p) 3) 15(a + b) + p 4) 15(a + p) + b
Решите уравнение 2 – 6х = 33 – 11(х + 2)
Ответ. ___________________
Упростите выражение  +
+  .
.
 2) 6 3) –
2) 6 3) – 4)
4) 
Площадь прямоугольного треугольника равна 6, а один из катетов равен 3. Найдите его гипотенузу.
Пусть а – длина второго катета, b – длина гипотенузы. Какая система уравнений соответствует условию задачи?




 = 6, 2) 3a = 6, 3) a2 – b2 = 9 4)
= 6, 2) 3a = 6, 3) a2 – b2 = 9 4)  =
= 
a2 + 9 = b2 b2 – a2 = 9 a = 1 b2 + a2 = 9
Упростите выражение  ·
·  · (
· (

 ).
).
Ответ. ______________________
Последовательности заданы несколькими первыми членами. Одна из них – арифметическая прогрессия. Найдите её.
4; 1; – 2; –5 3) 4; –2; 1; –
4; – 1; 2; –5 4) 4; 2; –1; –0,5
Из формулы s =  выразите переменную t. (все величины положительны).
выразите переменную t. (все величины положительны).
Ответ. _____________________
Графику функции у = –  принадлежит точка
принадлежит точка
(0; – 7) 2) (49;  ) 3) (–10; 0,7) 4) (14; 2)
) 3) (–10; 0,7) 4) (14; 2)
Найдите сумму квадратов корней уравнения х2 – 2х – 8 = 0
Ответ. ________________________
Определите. Какое из данных выражений тождественно равно выражению  – (х – у), х – у ≠0.
– (х – у), х – у ≠0.
2у 2) 2ху 3) 2ху + х + у 4) 
На склад прибыло 35 м3 древесины, что составляет  от заказа. Сколько места останется свободным на складе после прибытия всего заказанного объёма, если до прибытия первой части заказа оставалось 56 м3 свободного места.
от заказа. Сколько места останется свободным на складе после прибытия всего заказанного объёма, если до прибытия первой части заказа оставалось 56 м3 свободного места.
7 м3 2) 16 м3 3) 49 м3 4) 31 м3
Параболы у = х2 + 3х + 7 и у = х2 +2х + 6 пересекаются в одной точке. Вычислите координаты этой точки.
Ответ. ____________________________
Сократите дробь.
Ответ. ______________________
Из заданных геометрических прогрессий выберите ту, среди членов которой есть число 9.
bn = – 32 2) bn = 32 3) bn = 3 · 2n – 1 4) bn = 2 · 3n – 1
Автомобиль едет из А в В сначала 2 мин с горы, а затем 5 мин в гору. Обратный же путь он проделывает за 13 мин. Во сколько раз быстрее автомобиль едет с горы. Чем в гору?
Ответ. ________________________
Найдите наименьшее значение выражения (7х + 2у – 11)2 + (2х – 3у + 4)2 и значения х и у, при которых оно достигается.
Ответ. __________________________


 Получите свидетельство
Получите свидетельство Вход
Вход


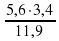 ?
?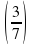 -2 равно
-2 равно 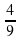 2) –
2) – 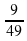 3) –
3) – 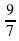 4)
4) 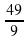
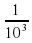 меньше числа
меньше числа 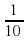 ?
?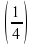 -2 – 4-3 : 4-5 + 20120
-2 – 4-3 : 4-5 + 20120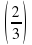 2 Б.
2 Б. 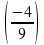 -1 В.
-1 В. 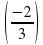 -2
-2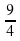 3)
3) 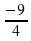
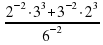 .
. 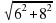 и b = 6+8
и b = 6+8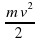 выразите m.
выразите m.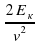 2) m =
2) m = 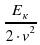 3) m =
3) m = 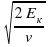 4) m =
4) m = 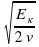
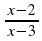 2)
2) 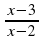 3)
3) 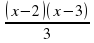 4)
4) 








 Разработка системы итогового повторения курса алгебры (0.24 MB)
Разработка системы итогового повторения курса алгебры (0.24 MB)
 0
0 1149
1149 196
196 Нравится
0
Нравится
0


