Цели урока:
- образовательные: формировать умение определять вид функций: четная или нечетная;
- развивающие: развитие алгоритмической культуры учащихся; способствовать развитию мыслительной деятельности учащихся, развитию математической речи, умения говорить красиво, грамотно, чётко, в нужном темпе; развивать память, умение слушать другого и понимать его речь;
- воспитательные: содействовать воспитанию интереса к математике, активности, организованности, формировать положительный мотив учения, развитие умений учебно-познавательной деятельности.
Структура урока:
Организационный момент.
Сообщение темы, постановка целей урока.
Устная работа.
Объяснение нового материала.
Формирование умений и навыков. (Работа в парах).
Самостоятельная работа по карточкам.
Итоги урока.
Домашнее задание.
Рефлексия.
Ход урока:
I.Организационный момент.
Здравствуйте, ребята! Садитесь. Я рада приветствовать вас сегодня на нашем уроке. Надеюсь, что сегодня на уроке нас ждет и успех, и радость. И мы, работая в коллективе, покажем свою одарённость.
Будьте внимательны в течение урока. Думайте, спрашивайте, предлагайте – так как дорогой к истине мы будем идти вместе.
II. Сообщение темы, постановка целей урока.
Откройте тетради и запишите число, «классная работа» и тему сегодняшнего урока «Четные и нечетные функции»
Слайд 1, 2
Эпиграфом нашего урока мы возьмем слова русского кораблестроителя, механика и математика Алексея Николаевича Крылова:
«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле» А.Н. Крылов
Цель нашей работы на уроке – познакомиться с важнейшим свойством функций – четностью и нечетностью; научиться определять вид данной функции, используя свои знания, полученные на предыдущих уроках, необходимо только их сейчас «привести в готовность».
III. Устная работа.
Слайд 3.
1. Устная работа
Чтобы привести свои знания «в готовность», ответьте на устные вопросы.
* Дайте определение числовой функции.
* Что называется областью определения числовой функции.
* Что называется областью значения числовой функции.
* Что называется графиком функции.
Слайд 4.
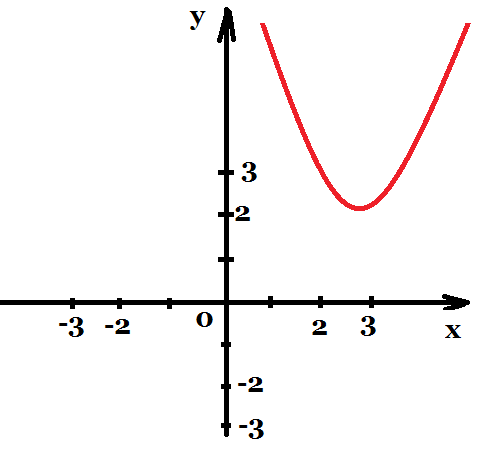
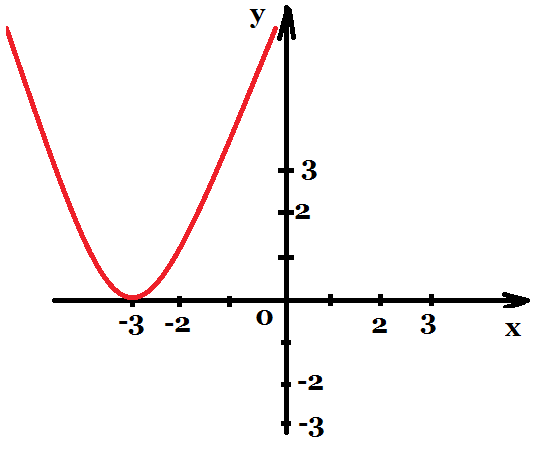
* Установите соответствие функции и ее графика:
IV. Объяснение нового материала.
1. Из множества числовых функций выделяют те, у которых область определения симметрична относительно начала координат.
Что значит «промежуток симметричен относительно начала координат»?
Слайд 5.
Промежутки, симметричны относительно начала координат, значит для любого х из этого промежутка (-х) также принадлежит этому промежутку.
Вопрос: Симметричны ли относительно начала координат промежутки: (-4;7); [-6;6]
2. Среди функций, у которых область определения симметрична относительно начала координат, выделяют четные и нечетные.
Слад 6. (формулировка определения четной функции)
Функция f называется ЧЕТНОЙ, если для любого х из ее области определения f(-x)=f(x)
Слайд7. (формулировка определения нечетной функции)
Функция f называется НЕЧЕТНОЙ, если для любого х из ее области определения f(-x)= -f(x)
Слайд 8.
Из свойств тригонометрических функций мы знаем, что:
Их области определения симметричны относительно начала координат.
Вывод: функции синуса, тангенса и котангенса – нечетные, косинуса – четная.
Слайд 9.
Свойства четных и нечетных функций.
При построении графиков четных и нечетных функций пользуются следующими их свойствами:
График четной функции симметричен относительно оси ординат.
2. График нечетной функции симметричен относительно начала координат.
Как проверить является функция четной или нечетной?
V. Формирование умений и навыков. (Работа в парах)
А теперь проверим, как вы сумеете определить вид функций.
Слайд 13, 14.
** Докажите, что функции являются четными
** Докажите, что функции являются нечетными
VI. Итог урока.
VII. Самостоятельная работа.
Слайд 15.
Карточки с заданиями раздаются каждому ученику. Слайд 15 дублирует задания.
Вариант 1.
Докажите, что функция f(x)=4х3+7х является нечетной.
Приведите пример четной функции.
Вариант 2.
Докажите, что функция f(x)=16х6 - 3х4 является четной.
Приведите пример нечетной функции.
VIII. Домашнее задание:
Слайд 16. № п.4 (1 ; №58 (a); №60 (б): 69(б)
XI. Рефлексия.
Слайд 17.
Оцените свою работу на уроке.
Удовлетворены ли вы результатом своей работы?
Слайд 18.
Спасибо, ребята, за урок.
Всем удачи!
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход







 ункция f называется ЧЕТНОЙ, если для любого х из ее области определения f(-x)=f(x)
ункция f называется ЧЕТНОЙ, если для любого х из ее области определения f(-x)=f(x) ункция f называется НЕЧЕТНОЙ, если для любого х из ее области определения f(-x)= -f(x)
ункция f называется НЕЧЕТНОЙ, если для любого х из ее области определения f(-x)= -f(x)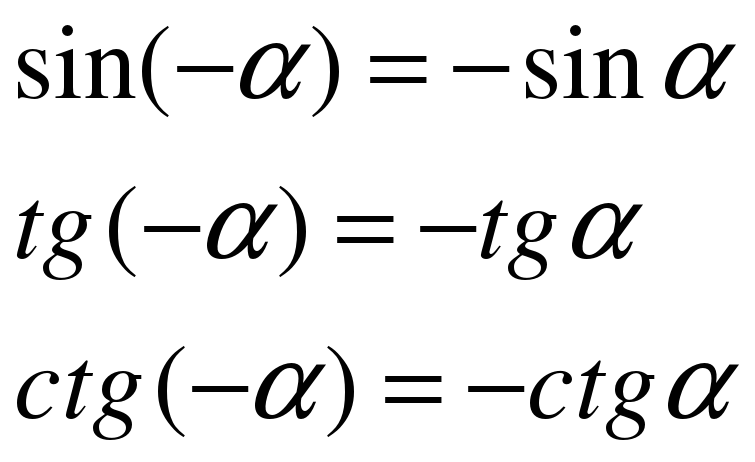
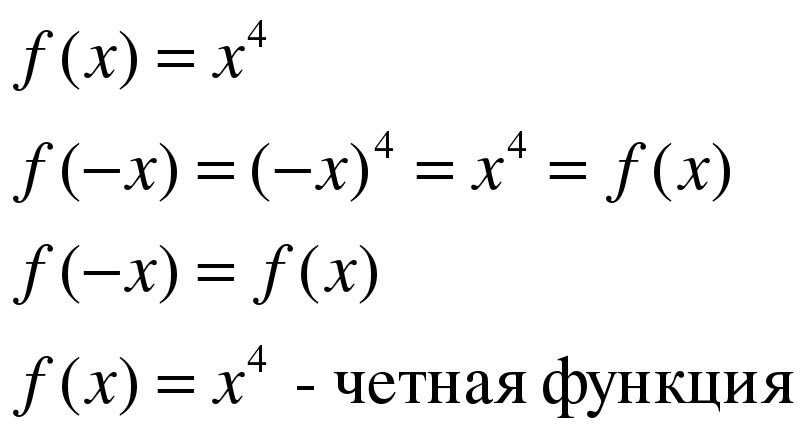 2.
2. 2.
2. 2.
2.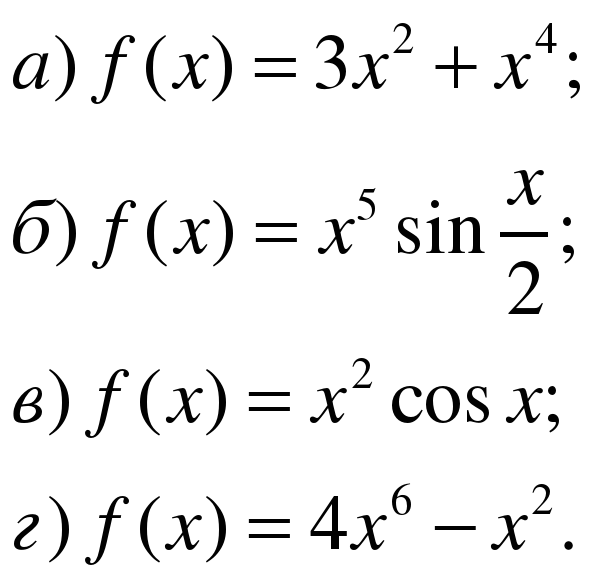











 Разработка урока "Четные и нечетные функции" (0.27 MB)
Разработка урока "Четные и нечетные функции" (0.27 MB)
 0
0 2856
2856 485
485 Нравится
0
Нравится
0


