Матрицы. Виды и свойства матриц. Операции над матрицами

Линейная алгебра – раздел высшей математики, который широко используется в теории вероятностей и математической статистике, в экономике, в исследовании операций и др.

Определение. Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера  m x n.

Числа, составляющие матрицу – элементы матрицы. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицы обозначаются заглавными буквами латинского алфавита (А, В, С, …), а элементы матрицы – строчными буквами с двойной индексацией (a_ij, где  i – номер строки, j –  номер столбца).

Матрицы записываются  (  ), или [  ],   или  ||     ||.

В презентации 30 слайдов.

Линейная алгебра. Основные сведения о матрицах. Виды и свойства матриц. Операции над матрицами .

Линейная алгебра – раздел высшей математики, который широко используется в теории вероятностей и математической статистике, в экономике, в исследовании операций и др.

1. Понятие матрицы

Определение. Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера тхп.

Числа, составляющие матрицу – элементы матрицы . Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицы обозначаются заглавными буквами латинского алфавита ( А, В, С, …), а элементы матрицы – строчными буквами с двойной индексацией ( , где i – номер строки,

j – номер столбца).

Матрицы записываются ( ), или [ ], или || ||.

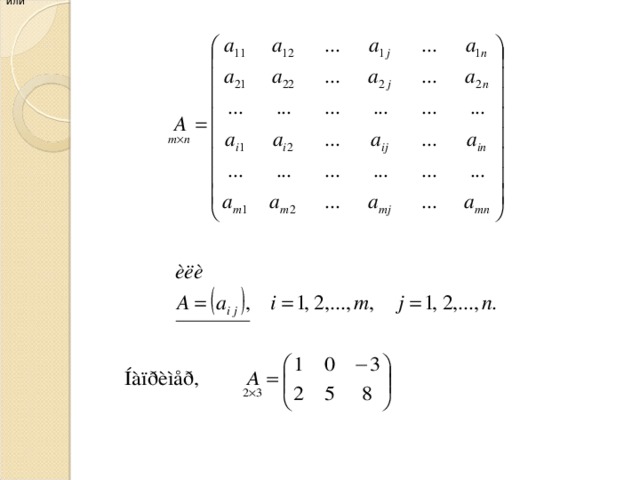
или

Определение. Две матрицы А и В одного размера называются равными , если они совпадают поэлементно, т.е. А = В , если для любых

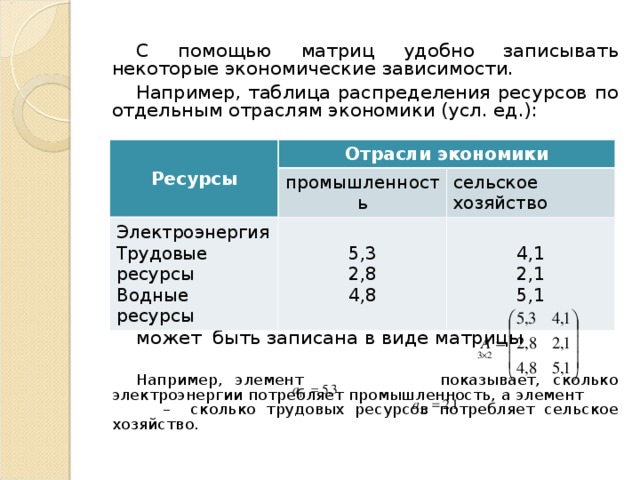
С помощью матриц удобно записывать некоторые экономические зависимости.

Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.):

может быть записана в виде матрицы

Например, элемент показывает, сколько электроэнергии потребляет промышленность, а элемент – сколько трудовых ресурсов потребляет сельское хозяйство.

Ресурсы

Отрасли экономики

промышленность

Электроэнергия

Трудовые ресурсы

Водные ресурсы

5,3

2,8

4,8

сельское хозяйство

4,1

2,1

5,1

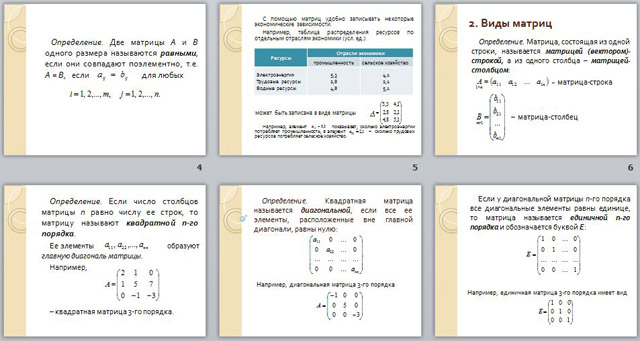
2. Виды матриц

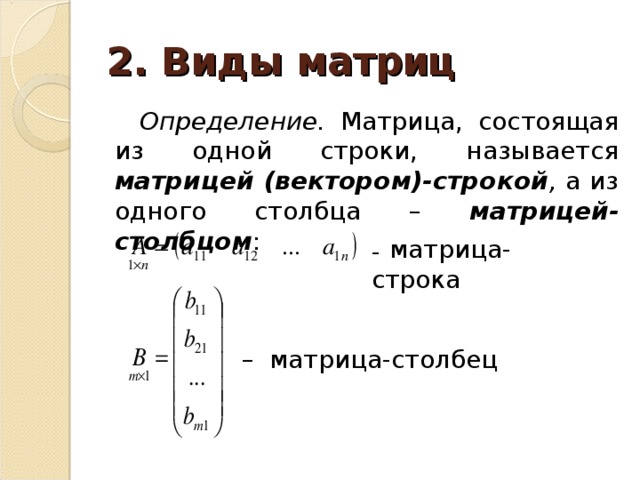
Определение. Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой , а из одного столбца – матрицей-столбцом :

– матрица-строка

– матрица-столбец

Определение. Если число столбцов матрицы п равно числу ее строк, то матрицу называют квадратной п-го порядка .

Ее элементы образуют главную диагональ матрицы .

Например,

– квадратная матрица 3-го порядка.

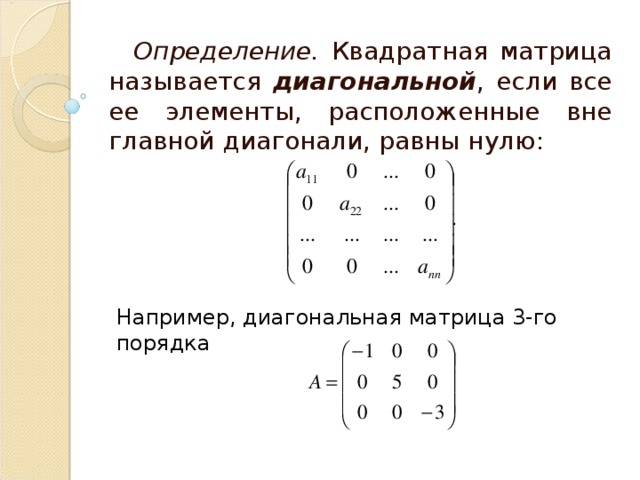
Определение. Квадратная матрица называется диагональной , если все ее элементы, расположенные вне главной диагонали, равны нулю:

Например, диагональная матрица 3-го порядка

Если у диагональной матрицы п -го порядка все диагональные элементы равны единице, то матрица называется единичной п-го порядка и обозначается буквой Е :

Например, единичная матрица 3-го порядка имеет вид

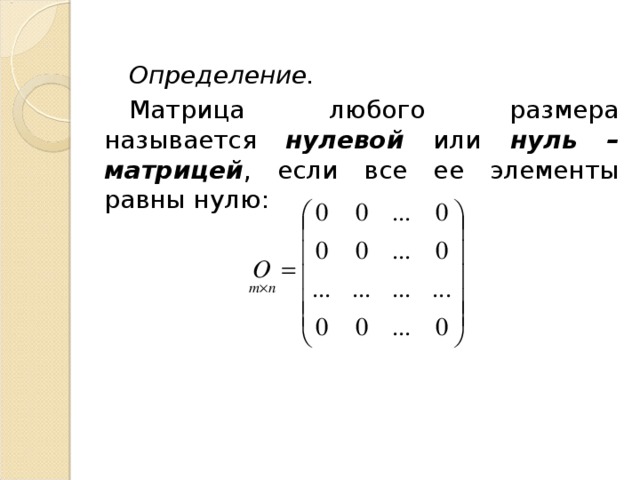
Определение.

Матрица любого размера называется нулевой или нуль – матрицей , если все ее элементы равны нулю:

Определение.

Квадратная матрица называется треугольной , если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Например,

3. Операции над матрицами

1) Умножение матрицы на число.

Определение. Произведением матрицы А на число λ называется матрица В= λ А , элементы которой для

Правило. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:

Например,

Если , то .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Например, .

Частный случай: произведение матрицы на число 0 есть нулевая матрица, т.е.

2) Сложение матриц

Определение. Суммой матриц А и В одинакового размера называется матрица С = А + В , элементы которой равны суммам элементов матриц А и В , расположенных на соответствующих местах, т.е. матрицы складываются поэлементно:

для

Например,

Частный случай: А + О = А.

3) Вычитание матриц

Определение. Разность двух матриц одинакового размера определяется через предыдущие операции:

А – В = А + (−1) ∙ В.

Например,

4) Умножение матриц.

Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В .

В результате умножения получится матрица С , у которой столько же строк, сколько их в матрице А , и столько же столбцов, сколько их в матрице В , т.е.

т.е.

Элементы матрицы С вычисляются по формуле:

,

т.е. каждый элемент равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В.

Правило. Для получения элемента , надо элементы i -й строки матрицы А умножить на соответствующие элементы j -го столбца матрицы В и полученные произведения сложить .

Пример.

Вычислить произведение матриц А ∙ В , где

Найдем размер матрицы-произведения

1) только квадратной матрицы А называется произведение т матриц, равных А , т.е. По определению: " width="640"

5) Возведение в степень

Определение. Целой положительной степенью А т ( т 1) только квадратной матрицы А называется произведение т матриц, равных А , т.е.

По определению:

Пример .

Возвести матрицу A в квадрат и в куб,

Решение.

6) Транспонирование матрицы -

переход от матрицы А к матрице , в которой строки и столбцы поменялись местами с сохранением порядка.

Матрица называется транспонированной относительно матрицы А:

Например,

если , то .

Свойства операции транспонирования:

4. Свойства операций над матрицами

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами:

• А + В = В + А
• ( А + В ) + С = А + ( В + С )
• А ( В + С ) = АВ +АС
• ( А + В ) С = АС + ВС
• А ( В ∙ С ) = ( АВ ) ∙ С
• А + О = А
• А – А = О

Однако имеются и специфические свойства матриц .

• Если произведение матриц А·В существует, то после перестановки сомножителей местами произведение матриц В·А может и не существовать.

• Например, существует,

а не существует.

2) Если даже произведения А·В и В·А существуют, то они могут быть матрицами разных размеров.

• Пример . Найти произведение матриц А·В и В·А :

3) Когда оба произведения А·В и В·А существуют и оба – матрицы одинакового размера, коммутативный (переместительный) закон умножения, вообще, не выполняется, т.е. .

Пример. Найти произведение матриц А·В и В·А , где

Решение.

• Частный случай. Коммутативным законом обладает произведение любой квадратной матрицы А п- го порядка на единичную матрицу того же порядка, причем это произведение равно А :

• Т.о., единичная матрица при умножении играет ту же роль, что и число 1 при умножении чисел.

4) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что А·В = О , не следует, что А= О или В= О .

Например,