Лінійна алгебра

Презентация на украинском языке.

Данный тематический модуль - это электронный интерактивный продукт по высшей математике, позволяющий студенту самостоятельно проработать теоретический материал, научиться по данному образцу вычислять определители и решать системы уравнений, а также проверить свои знания, ответив на контрольные вопросы. В этом модуле рассмотрены конкретные прикладные задачи, которые стимулируют учебную деятельность и позволяют понять необходимость изучения данной темы.

Міністерство аграрної політики України

Бучацький коледж

Подільського ДАТУ

Лінійна

алгебра

тематичний модуль

Вища

математика

Викладач:

М.Д. Фасолько

Анотація

Даний тематичний модуль – це електронний інтерактивний продукт з вищої математики, який дає можливість студенту самостійно опрацювати теоретичний матеріал, навчитися за поданими зразками обчислювати визначники і розв’язувати системи алгебраїчних рівнянь, а також перевірити свої знання, відповівши на контрольні запитання. В цьому модулі розглянуто конкретні прикладні задачі, які стимулюють навчальну діяльність і дають змогу зрозуміти необхідність вивчення даної теми.

М.Д. Фасолько " Вища математика "

Матриці. Вектори.

Визначники. Системи.

• 1. Матриці та вектори.
• 2. Визначники.
• 3. Системи лінійних алгебраїчних рівнянь .

ПЛАН

М.Д. Фасолько " Вища математика "

М.Д. Фасолько - Лекції

М О Т И В А Ц І Я

Лінійна алгебра – це розділ математики, який вивчає матриці, визначники та системи лінійних рівнянь.

В процесі дослідження багатьох питань економіки, природознавства, техніки доводиться розв’язувати системи лінійних алгебраїчних рівнянь, виконувати дії над матрицями, обчислювати визначники. Наприклад, при розрахунку кількості деталей для комплектування виробів, зарплатні робітникам, які ці вироби виготовляють, використовують дії множення матриць.

Складаючи модель міжгалузевого балансу в економіці, застосовують звичайні лінійні рівняння, що об’єднані в систему.

Тому, вивчаючи цей модуль, нам потрібно оволодіти знаннями і навичками, які дадуть можливість вирішувати на практиці виробничі задачі.

М.Д. Фасолько " Вища математика "

Означення

матриці

Означення. Матрицею розміром n×m називається прямокутна таблиця чисел:

М.Д. Фасолько " Вища математика "

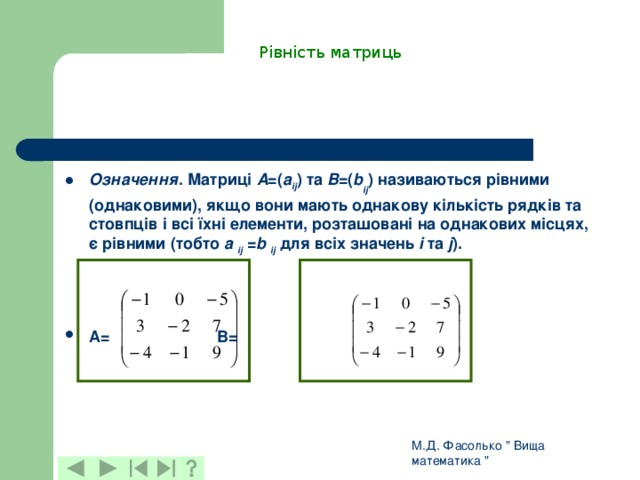
Рівність матриць

• Означення . Матриці A =( a ij ) та B =( b ij ) називаються рівними (однаковими), якщо вони мають однакову кількість рядків та стовпців і всі їхні елементи, розташовані на однакових місцях, є рівними (тобто a ij = b ij для всіх значень i та j ).

• А= В=

М.Д. Фасолько " Вища математика "

Сума і добуток

• Означення . Добутком матриці A =( a ij ) на число k називається матриця B=k  A вигляду
• B=k  A =( k  a ij ).

• Означення . Сумою двох матриць A =( a ij ) та B =( b ij ) з однаковою кількістю рядків та стовпців називається матриця C=A+B , де

c ij =a ij +b ij

М.Д. Фасолько " Вища математика "

Квадратна

та одинична

матриці

тобто ця матриця має вигляд

• Матриця називається квадратною, якщо кількість її рядків співпадає із кількістю стовпців ( n=m ).
• Квадратна матриця E =( eij ) називається одиничною, якщо

М.Д. Фасолько " Вища математика "

Добуток

матриць

• Означення . Добутком матриці

на матрицю називається матриця

елементи якої обчислюються за формулою

М.Д. Фасолько " Вища математика "

Приклади

• 1. Нехай та .

• Тоді

• 2. Нехай, крім того,

• Тоді

D  C - не має сенсу,

М.Д. Фасолько " Вища математика "

Приклади

С

***

М.Д. Фасолько " Вища математика "

Властивості

дій

• Виконуються такі властивості додавання та множення матриць:
• Е  А = А  Е = А (множення на одиничну матрицю);
• О  А = А  О = О (множення на нульову матрицю);
• A+B = B+A (комутативна властивість додавання);
• A+(B+C)=(A+B)+ C (асоціативна властивість додавання);
• (A+B)C = AC+BC ( дистрибутивна властивість)

М.Д. Фасолько " Вища математика "

Транспонована

матриця

Означення.  Матрицею   A Т , транспонованою до матриці

називається матриця .

Виконуються такі властивості:

• (AB) Т = B Т A Т ;
• (  A+  B) Т =  A Т +  B Т ;
• (A Т ) Т = A .

М.Д. Фасолько " Вища математика "

Матриця-рядок

Матриця-стовпець

• Частковим випадком матриці є вектор (упорядкована послідовність чисел). Розрізняють вектор-рядок (матрицю-рядок) та

вектор-стовпець (матрицю-стовпець)

Добуток матриці на вектор обчислюється за загальним означенням множення матриць:

М.Д. Фасолько " Вища математика "

Приклад

• Приклад . Для виготовлення виробів W1 та W2 потрібні вузли v1 та v2 . Для виготовлення цих вузлів, в свою чергу, відповідно, потрібні деталі d1 , d2 та d3 у кількостях, що наведені у таблицях:

Вироби

Кількість вузлів

W1

v1

W2

v2

2

1

3

Вузли

Кількість деталей

4

v1

d1

v2

2

d2

1

d3

1

0

0

3

М.Д. Фасолько " Вища математика "

АНАЛІЗ

Обчислити кількість деталей, що потрібні для виготовлення кожного із виробів W1 та W2 .

• На основі аналізу цих таблиць бачимо, що шукана кількість деталей обчислюється як добуток матриць

М.Д. Фасолько " Вища математика "

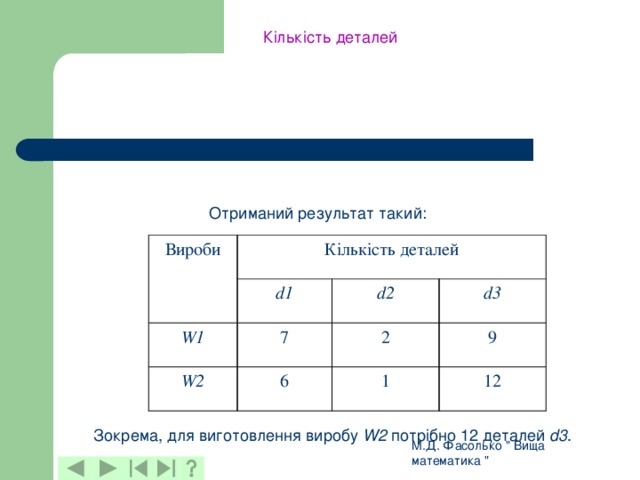
Кількість деталей

Отриманий результат такий:

Вироби

Кількість деталей

W1

d1

W2

d2

7

6

d3

2

9

1

12

Зокрема, для виготовлення виробу W2 потрібно 12 деталей d3 .

М.Д. Фасолько " Вища математика "

Вхідна

інформація

• Приклад . Нарахувати заробітну плату, яку потрібно виплатити на кожне замовлення, якщо вхідна інформація задана у таблицях:

Таблиця А

Виріб

Затрати робочого часу на робочих місцях, год.

W1

1

W2

2

0,8

W3

1,3

3

2,1

4

0,5

1,2

1,1

3,0

2,8

1,0

0,2

2,5

1,8

М.Д. Фасолько " Вища математика "

Вхідна

інформація

• Таблиця С

Таблиця B

Робоче місце

1

Погодинна заробітна плата, грн.

2

1,30

3

1,25

4

1,40

1.45

Замовлення

Кількість виробів

Z1

W1

Z2

5

W2

Z3

4

7

W3

3

6

0

2

2

1

М.Д. Фасолько " Вища математика "

Затрати часу

• Помноживши матрицю B на матрицю A , отримуємо затрати часу на робочих місцях щодо кожного замовлення:

Замовлення

Затрати робочого часу на робочих місцях, год.

Z1

1

Z2

16,4

2

Z3

17

3

5,4

33,1

4

10,4

8,5

9,8

21,8

14,6

15,6

15,3

20,2

Справді,

М.Д. Фасолько " Вища математика "

Витрати на зарплату

• Перемноживши отриману матрицю на вектор (матрицю-стовпець) C , обчислимо витрати на зарплату щодо кожного із замовлень:

Замовлення

Z1

Витрати на зарплату

Z2

120,52

56,36

Z3

80,01

Отже, витрати на зарплату обчислюються як добуток матриць:

М.Д. Фасолько " Вища математика "

Поняття

визначника

Означення . Визначником (детермінантом) матриці другого

порядку

називається число

Означення . Визначником (детермінантом) матриці третього порядку

    називається  число  D ( A )=

Приклади:

М.Д. Фасолько " Вища математика "

.

Властивості

визначників

• Означення . Визначником квадратної матриці A розміру n×n називається число

Легко перевірити, що означення визначника другого та третього порядку задовольняє загальне означення.

Множина визначників задовольняє такі властивості:

• У разі транспонування матриці значення визначника не змінюється:

2. У випадку перестановки двох довільних рядків (або двох довільних стовпців) знак визначника змінюється на протилежний:

М.Д. Фасолько " Вища математика "

.

Властивості

визначників

3. Якщо всі елементи одного рядка (стовпця) матриці є пропорційними до елементів другого рядка (стовпця) цієї матриці, то її визначник дорівнює нулю:

, оскільки елементи третього рядка є вдвічі

більшими від елементів першого.

4. Якщо всі елементи рядка (стовпця) помножити на якесь число, то визначник теж помножиться на це ж число:

.

М.Д. Фасолько " Вища математика "

Властивості

визначників

5. Якщо до елементів деякого рядка (стовпця) додати елементи іншого рядка (стовпця), помножені на довільне число, то значення визначника не зміниться:

.

М.Д. Фасолько " Вища математика "

МІНОРИ

Означення . Мінором M ij елемента a ij визначника

називається визначник розміру (n-1)×(n-1) ,який утворюється з

визначника

викреслюванням i -го рядка та j -го стовпця.

Приклад . У визначнику

визначники другого порядку

є відповідно мінорами елементів a 1 , b 1 та c 1 .

М.Д. Фасолько " Вища математика "

Алгебраїчне доповнення

• Означення .

Алгебраїчним доповненням A ij елемента a ij називається його мінор, узятий зі знаком (+) або (-) так:

якщо сума (i+j) номерів рядка i та стовпця j є парною, то потрібно взяти знак (+), якщо ж ця сума непарна – то знак (-).

Для визначника довільного порядку виконується така теорема.

Теорема . Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення цих елементів.

Зокрема,

= a 11 A 11 + a 12 A 12 +…+ a 1n A 1n . (1.5)

М.Д. Фасолько " Вища математика "

Обчислення

Приклад . Обчислити визначник

.

Згідно з означенням  =2  8  5+5  0  1+3  3  (-2)-1  8  (-2)-5  3  5-2  0  3=3.

За теоремою (розкладаємо визначник за елементами другого рядка) отримуємо той самий результат:

 = a 21 A 21 + a 22 A 22 + a 23 A 23 = a 21 (- M 21 )+ a 22 M 22 + a 23 (- M 23 ) =

=(-3)  31+8  12+(-0)  1 = 3

=

Таким способом обчислення визначників високих порядків можна послідовно зводити до відшукання визначників щораз менших порядків.

М.Д. Фасолько " Вища математика "

Приклад

Матриця

має три мінори третього порядку (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r ( A )=2.

М.Д. Фасолько " Вища математика "

0), що . Якщо ж із рівності випливає той факт, що k 1 = k 2 =…= k m =0, то система називається лінійно незалежною . М.Д. Фасолько " Вища математика " " width="640"

Лінійна

залежність та незалежність

Розглянемо систему векторів

у n -вимірному просторі. Ця система називається лінійно залежною , якщо існують такі числа k 1 ,… k m (не всі з яких одночасно дорівнюють нулю: k 1 2 + k 2 2 +…+ k m 2 0), що

.

Якщо ж із рівності

випливає той факт, що k 1 = k 2 =…= k m =0, то система називається

лінійно незалежною .

М.Д. Фасолько " Вища математика "

 0 і одночасно . Приклад . Система векторів та є лінійно незалежною, бо рівність , тобто , виконується тільки при k 1 = k 2 = 0 . Легко бачити, що при m  n система векторів завжди є лінійно залежною. М.Д. Фасолько " Вища математика " " width="640"

Приклади

Приклад .

Система векторів

є лінійно залежною, бо існують числа k 1 =1, k 2 =1/2, k 3 =1 такі, що k 1 2 + k 2 2 +…+ k m 2  = 1+1/4+1  0 і одночасно

.

Приклад . Система векторів

та

є лінійно незалежною, бо рівність

, тобто

,

виконується тільки при k 1 = k 2 = 0 .

Легко бачити, що при m  n система векторів завжди є лінійно залежною.

М.Д. Фасолько " Вища математика "

Системи

лінійних алгебраїчних рівнянь

Розглянемо систему двох рівнянь з двома невідомими

Розглянемо систему двох рівнянь з двома невідомими

.

Кожне з цих рівнянь задає деяку пряму на площині. Позначимо основну матрицю цієї системи через

.

, а розширену матрицю ­ через

М.Д. Фасолько " Вища математика "

Число розв'язків

Можливі три такі випадки:

- ранг матриці r ( A )=2. Вектори ( a 1; b 1; c 1) та ( a 2; b 2; c 2), отже, є лінійно незалежними і система має єдиний розв’язок ( x 0; y 0). Геометрично маємо дві прямі на площині, які перетинаються в одній точці;

- ранг розширеної матриці r ( B )=2, а ранг основної r ( A )=1. Вектори ( a 1; b 1; c 1) та ( a 2; b 2; c 2) є лінійно незалежними, а вектори ( a 1; b 1) та ( a 2; b 2) – лінійно залежними. Рівняння системи ­ це дві паралельні прямі, Отже, система не має розв’язків;

- ранг як основної, так і розширеної матриці дорівнює одиниці: r ( A )= r ( B )=1. Вектори ( a 1; b 1; c 1) та ( a 2; b 2;c2) є лінійно залежними. Геометрично маємо дві прямі, які збігаються. Система має безліч розв’язків.

М.Д. Фасолько " Вища математика "

С И С Т Е М И

Розглянемо тепер систему трьох рівнянь з трьома невідомими

.

Кожне рівняння цієї системи задає деяку площину в просторі.

Можливі такі випадки:

• усі три площини перетинаються в одній точці ( x 0 ; y 0 ; z 0 ). Ранг r ( A )=3. Система має єдиний розв’язок ( x 0 ; y 0 ; z 0 );
• усі три площини перетинаються по одній прямій (при цьому площини можуть збігатися). Ранг r ( A )r ( B )
• хоча б дві площини є паралельними між собою ( r ( A )r ( B )=3). Система розв’язків не має.

М.Д. Фасолько " Вища математика "

Системи двох рівнянь

з трьома невідомими

• Розглянемо систему двох рівнянь з трьома невідомими

Можливі лише такі випадки:

• дві площини, задані цими рівняннями, паралельні. Це є тоді, коли ранг звичайної (основної) матриці r ( A )=1, а ранг розширеної –  r ( B )=2. Система розв’язків не має;
• обидві площини співпадають. Вектори ( a 1 ; b 1 ; c 1 ; d 1 ) та ( a 2 ; b 2 ; c 2 ; d 2 ) лінійно залежні. Система має безліч розв’язків;
• площини перетинаються по прямій. Ранги обох матриць r ( A )= r ( B )=2. Ці ранги є меншими від кількості невідомих системи. Система, отже, має безліч розв’язків.

Зазначимо, що множиною розв’язків у другому випадку є площина, а в третьому – пряма. Тому розв’язати систему двох рівнянь з трьома невідомими ‑ означає описати аналітично множину всіх розв’язків.

М.Д. Фасолько " Вища математика "

Приклад

Розв’язати систему

Перенесемо змінну x у праву частину:

.

Помножимо перше рівняння на -2 і додамо до другого:

4 z = -28

Помножимо перше рівняння на 2 і додамо до другого:

-8 y = 32-4 x

Розв’язуючи отриману систему

знаходимо:

y = (1/2) x -4 ; z = -7.

Отже, загальний розв’язок початкової системи має вигляд

{( x ; -4+0,5 x ;7)| x  R }. Надаючи параметру x різних значень, ми отримуємо конкретні розв’язки. Наприклад, при x =1 розв’язком є трійка чисел

(1; -3,5; -7), при x =0 – (0; -4; -7) , а при x =5 – (10; 1; -7). Трійку чисел (2; 2; 2) не можна отримати при жодному значенні параметра, отже, розв’язком системи вона не є.

М.Д. Фасолько " Вища математика "

Методи розв’язування

Розглянемо методи розв’язування систем n лінійних рівнянь з n невідомими

• Розглянемо методи розв’язування систем n лінійних рівнянь з n невідомими

.

Одним із способів є використання оберненої матриці :

.

М.Д. Фасолько " Вища математика "

МАТРИЧНИЙ

СПОСІБ

М.Д. Фасолько " Вища математика "

РОЗВ'ЯЗАННЯ

М.Д. Фасолько " Вища математика "

РОЗВ'ЯЗАННЯ

М.Д. Фасолько " Вища математика "

ФОРМУЛИ КРАМЕРА

• Розглянемо також правило Крамера .

Нехай  ‑ визначник матриці

.

Введемо позначення

( i =1,…, n ).

Виконується така  теорема : Якщо  0, то система

має єдиний розв’язок, який знаходиться за такими формулами (Крамера):

. (1.7)

Якщо  =0 і в множині {  1 ,…,  n } є ненульові елементи, то система рівнянь розв’язків не має. Якщо ж  =  1 =…  n =0 , то система має безліч розв’язків.

М.Д. Фасолько " Вища математика "

Розв'язати

систему

М.Д. Фасолько " Вища математика "

Розв'язати

систему

• Приклад.

.

Тут

Отже, x 1 =81/27=3; x 2 =(-108)/27=-4; x 3 =(-27)/27=-1; x 4 =27/27=1.

М.Д. Фасолько " Вища математика "

Метод Жордана-Гауса

• Розглянемо схему Жордана-Гауса на прикладі розв’язування конкретної системи

,

яку у матричному вигляді записують так:

.

Початкова таблиця має такий вигляд:

.

Числа -2 та -3 ‑ це елементи другого та третього рядка (взяті з протилежним знаком), які розташовані в тому стовпці, де в першому рядку є число 1.

М.Д. Фасолько " Вища математика "

Метод Жордана-Гауса

Множимо перший рядок на числа -2 та -3 й отримуємо, відповідно, вектори (-2; -4; 6; 12) та (-3; -6; 9; 18). Додаємо ці вектори до другого і третього рядків:

.

Ділимо всі елементи другого рядка на -5, роблячи діагональний елемент таблиці одиничним:

.

М.Д. Фасолько " Вища математика "

Метод Жордана-Гауса

• Розпочинаємо наступний етап методу

• На останньому кроці множимо третій рядок на 1/5 та 1/7 і додаємо утворені вектори (0;0;1/5;3/5) і (0;0;7/5;21/5) до першого та другого рядка:

. Множимо другий рядок на -2 та на 4 й отримуємо вектори (0; -2; 14/5; 22/5) і (0; 4;-28/5;-44/5). Додаємо ці вектори до першого та третього рядків:

тобто отримуємо систему рівнянь

.

,

і робимо ще один діагональний елемент одиницею (ділимо на 22/5):

, розв’язками якої є числа x 1 = -1; x 2 =2; x 3 =3.

Якщо під час обчислень у схемі Жордана-Гауса деякий рядок повністю стає нульовим ( 0 0 0 | 0 ), то це є ознакою того факту, що система має безліч розв’язків.

М.Д. Фасолько " Вища математика "

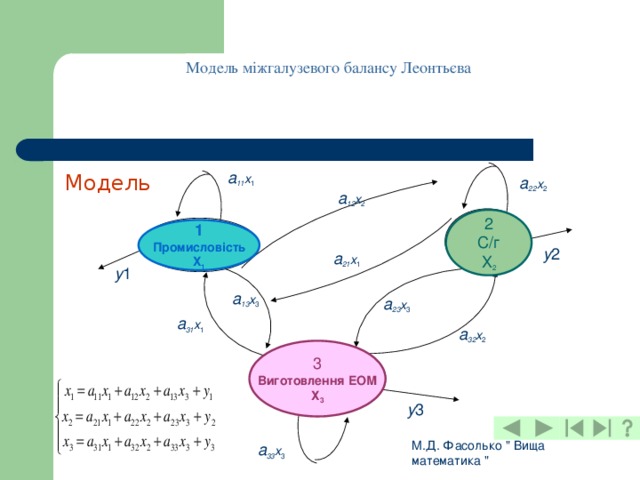
Модель міжгалузевого балансу Леонтьєва

a 11 x 1

Модель

a 22 x 2

a 12 x 2

2

С/г

Х 2

1

Промисловість

Х 1

y 2

a 21 x 1

y 1

a 13 x 3

a 23 x 3

a 31 x 1

a 32 x 2

3

Виготовлення ЕОМ

Х 3

y 3

a 33 x 3

М.Д. Фасолько " Вища математика "

ТРИ ГАЛУЗІ

Нехай у деякій державі є три галузі господарства: промисловість, сільське господарство та виготовлення ЕОМ. Нехай x 1, x 2, x 3 ‑ обсяги виробництва у цих галузях. Нехай також y 1, y 2 y 3 ‑ обсяги кінцевого виробництва (виробництва на продаж, виробництва без внутрішнього споживання) цих галузей.

Нехай aij ‑ кількість одиниць продукції i -ої галузі, яка йде на виробництво однієї одиниці продукції j -ої галузі. Зокрема, кожна одиниця продукції сільськогосподарської галузі (галузі номер 2) використовує a 12 одиниць продукції промисловості (галузі номер 1) та a 32 одиниць продукції галузі, яка виготовляє комп’ютери.

М.Д. Фасолько " Вища математика "

РІВНЯННЯ БАЛАНСУ

Отже, для другої галузі маємо таке рівняння балансу:

x 1 = a 11 x 1 + a 12 x 2 + a 13 x 3 + y 1

Записавши аналогічні рівняння для кожної із галузей, отримуємо систему лінійних рівнянь:

.

Цю систему для випадку n змінних записують також у вигляді

та в матричному вигляді

(1.8)

М.Д. Фасолько " Вища математика "

КІНЦЕВА

ПРОДУКЦІЯ

• Побудована система міжгалузевого балансу (модель Леонтьєва) дає змогу за обсягами виробництва в окремих галузях контролювати їхній кінцевий продукт та навпаки.
• Із формули (1.8) випливає, що вектор кінцевої продукції в моделі Леонтьєва визначається формулою

(1.9)

вектор загального випуску –

. (1.10)

М.Д. Фасолько " Вища математика "

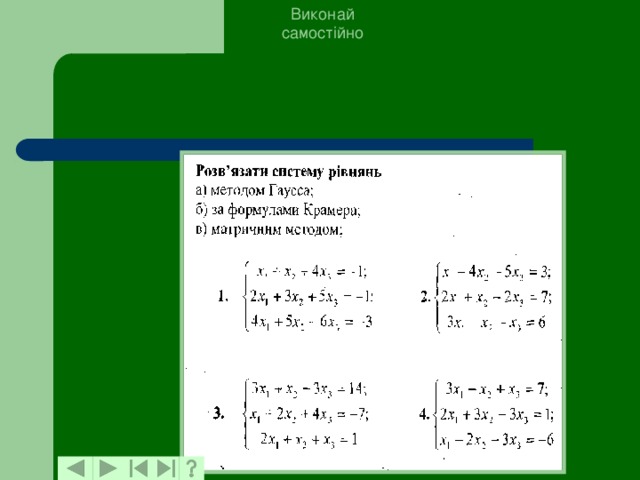
Виконай

самостійно

М.Д. Фасолько " Вища математика "

виконай

самостійно

М.Д. Фасолько " Вища математика "

Контрольні запитання

• Розв’язування систем лінійних рівнянь за допомогою формул Крамера.
• Модель міжгалузевого балансу.
• Метод Жордано-Гаусса.
• Транспонована матриця.
• Що таке мінор?
• Алгебраїчні доповнення.
• Лінійна залежність та незалежність.
• Рівняння балансу.

• Що таке матриця?
• Які матриці наз. рівними?
• Операції над матрицями, їхні властивості.
• Матриця-рядок. Матриця-стовпець
• Розв’язування систем лінійних рівнянь за допомогою оберненої матриці.
• Визначник другого та третього порядку.
• Властивості визначників.
• Обчислення визначника n -го порядку.
• Система двох лінійних рівнянь з двома невідомими.
• Система двох лінійних рівнянь з трьома невідомими
• Система трьох лінійних рівнянь з трьома невідомими

М.Д. Фасолько " Вища математика "

СПИСОК ЛІТЕРАТУРИ

• Барковський В., Барковська Н . Математика для економіста. – К., 1997.‑ Т.1‑3.
• Бугір М . Математика для економістів. – Тернопіль, 1998.
• Михайленко В., Федоренко Н . Математичний аналіз для економістів. – К., 1999.
• Нікбахт Е., Гроппелі А . Фінанси. ‑ К., 1993.
• Nicholson R.N . Mathematics for Business and Economics. ‑ 1986.
• Завада О . Методичні вказівки до виконання контрольних робіт з курсу “Математика для економіста”. –Львів, 2000.

М.Д. Фасолько " Вища математика "

Завершити