Презентация с материалами для изучения темы "Отношения" (На украинском языке)

Презентация с материалами для изучения темы "Отношения" (На украинском языке)



Зміст навчального матеріалу
Відношення.
Основна
властивість
Відношення.

Відношення
Частку двох чисел
називають відношенням цих чисел.
Відношення показує,
у скільки разів одне число більше від другого
або яку частину становить одне число від другого.
3:5
2,7:0,4
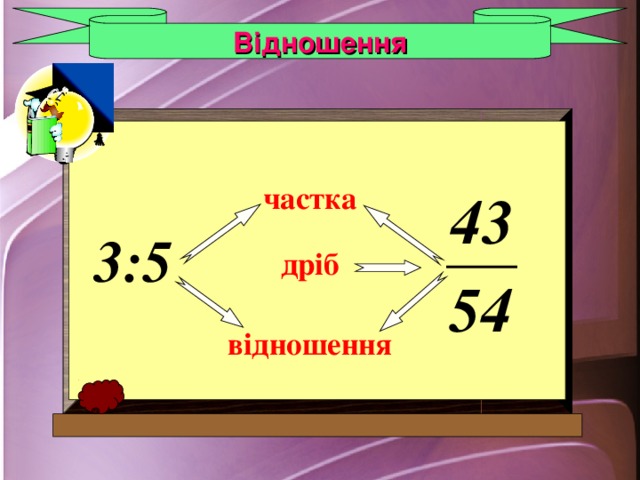
Відношення
частка
3:5
дріб
відношення

Основна властивість
відношення
Відношення двох чисел не зміниться,
якщо кожне з них помножити або поділити
на одне й те саме число,
відмінне від нуля.
Обидва члени пропорції можна поділити
на їх спільний дільник.
Відношення дробових чисел можна замінити
відношенням натуральних чисел.

Пропорція.
Основна
властивість
пропорції.

Пропорція
Рівність двох відношень
називають пропорцією .
a : b = c : d , або
при b ≠ 0 і d ≠ 0
a, d – крайні члени пропорції
c, b – середні члени пропорції

Основна властивість
пропорції
Добуток крайніх членів кожної пропорції
дорівнює добутку її середніх членів.
Якщо a : b = c : d то a · d = c · b
4 : 2 = 8 : 4 то 4 · 4 = 8 · 2

Невідомий член
пропорції
Щоб знайти невідомий крайній член пропорції,
досить добуток її середніх членів поділити
на відомий крайній.
Щоб знайти невідомий середній член пропорції,
досить добуток її крайніх членів поділити
на відомий середній.

Розв’язування
рівнянь
на основі
властивості
пропорції.

Розв'яжіть рівняння
x : 2 = 3 : 11

Розв'яжіть рівняння

Розв'яжіть рівняння

Випадкова
подія.
Імовірність
випадкової
події.

Подія
Подія – те, що діється, відбувається, трапляється.
Подія – це явище, яке обов'язково спостерігалось
більшу чи меншу кількість разів при багаторазовому
повторенні досліду.
Підкидаємо монету – дослід,
поява орла – подія.
Дістаємо лампу з коробки – дослід,
лампа бракована – подія.
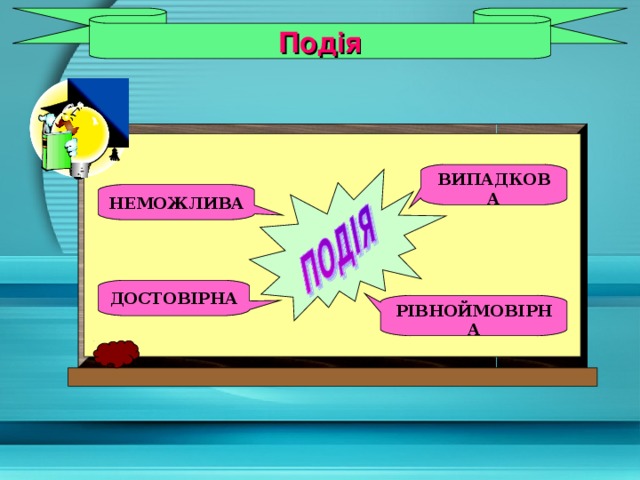
Подія
ВИПАДКОВА
НЕМОЖЛИВА
ДОСТОВІРНА
РІВНОЙМОВІРНА

Подія
Ймовірністю події називають відношення кількості
сприятливих для цієї події результатів
до кількості всіх можливих результатів.
де А – подія;
Р(А) – ймовірність події
N – загальна кількість рівноможливих і несумісних подій
N (А) – кількість подій, які сприяють події

Відсоткове
відношення
двох чисел.
Відсоткові розрахунки.
Задачі економічного
змісту.

Відсоткове відношення
Якщо відношення двох чисел виражають у відсотках,
то його називають відсотковим відношенням .
Один відсоток – це одна сота частини
1% = 0,01 50% = 0,5
100% = 1 200% = 2

Відсоткове відношення
Існує три основні види задач на відсотки
знаходження відсотків від числа
знаходження числа за відсотком
знаходження відсоткового відношення двох чисел
за І день
? га
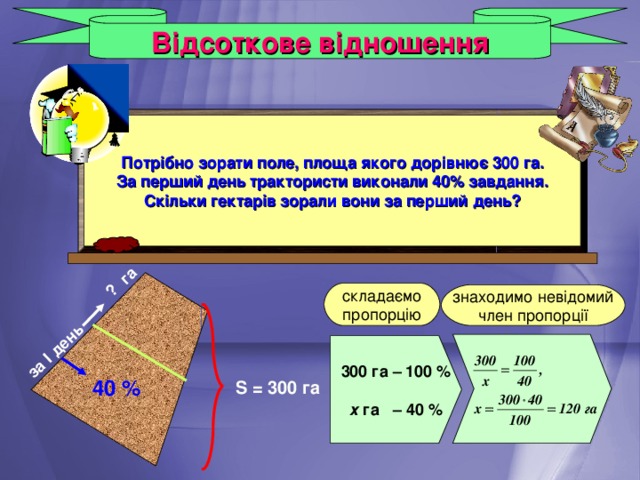
Відсоткове відношення
Потрібно зорати поле, площа якого дорівнює 300 га.
За перший день трактористи виконали 40% завдання.
Скільки гектарів зорали вони за перший день?
складаємо
пропорцію
знаходимо невідомий
член пропорції
300 га – 100 %
х га – 40 %
40 %
S = 300 га
за І день
120 га
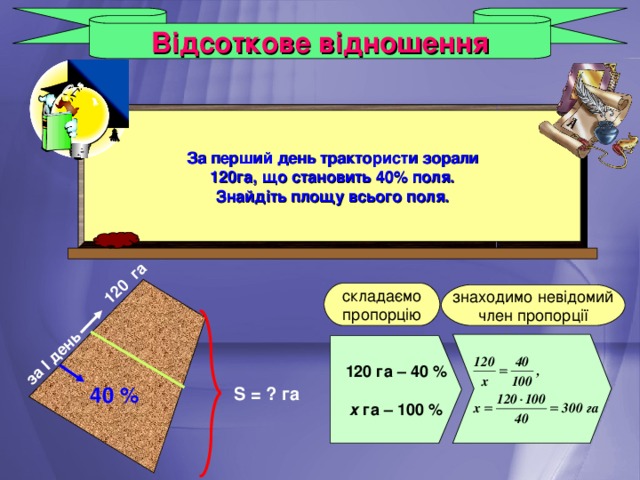
Відсоткове відношення
За перший день трактористи зорали
120га , що становить 40% поля.
Знайдіть площу всього поля.
складаємо
пропорцію
знаходимо невідомий
член пропорції
120 га – 40 %
х га – 100 %
40 %
S = ? га
за І день
120 га
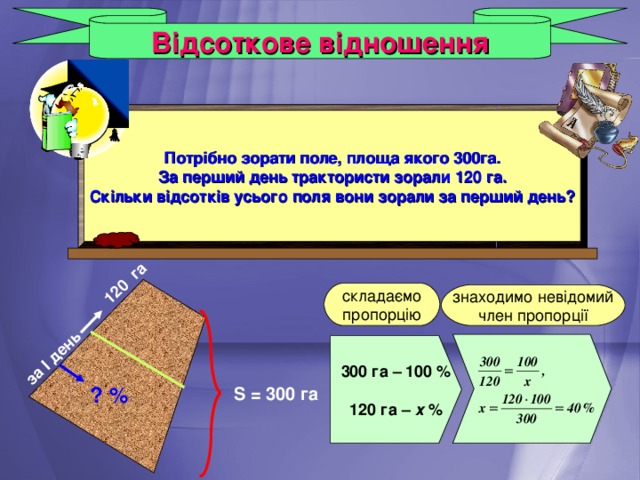
Відсоткове відношення
Потрібно зорати поле, площа якого 300га.
За перший день трактористи зорали 120 га.
Скільки відсотків усього поля вони зорали за перший день?
складаємо
пропорцію
знаходимо невідомий
член пропорції
300 га – 100 %
120 га – х %
? %
S = 300 га

Пряма
пропорційна
залежність.

Пряма пропорційна залежність
Дві величини називають пропорційними ,
якщо зі збільшенням (зменшенням) значень
однієї з них у кілька разів значення другої
збільшується (зменшується) у стільки само разів.
Швидкість, км/год
Час, год
60
Шлях, км
60
1
60
60
2
3
60
120
4
180
240

Обернено пропорційна залежність
Дві величини називають обернено пропорційними ,
якщо зі збільшенням (зменшенням) значень
однієї з них у кілька разів значення другої
зменшується (збільшується) у стільки само разів.
Швидкість, км/год
Час, год
50
Шлях, км
60
6
300
100
5
4
150
300
3
300
300

Задачі на
пропорційний
поділ.

Задачі на пропорційний поділ
Щоб поділити число на частини, пропорційні
даним числам, треба поділити його на суму
даних чисел і знайдену частку помножити
на кожне з них.
Дріт завдовжки 60 м розрізали на 3 частини,
довжини яких пропорційні числам 2, 3 і 5.
Знайдіть довжини цих частин дроту.

Задачі на пропорційний поділ
Окремим видом задач на пропорційний поділ
є задачі на знаходження двох чисел
за їх сумою і відношенням.
Задача 1. Поле площею 100 га поділили на дві
частини, площі яких пропорційні числам 2 і 3.
Знайдіть площі цих частин.
Задача 1. Поле площею 100 га поділили на дві
частини, площі яких відносяться як 2 : 3.
Знайдіть площі цих частин.

Коло.
Довжина кола.
Круг.
Площа круга.
Круговий
сектор.
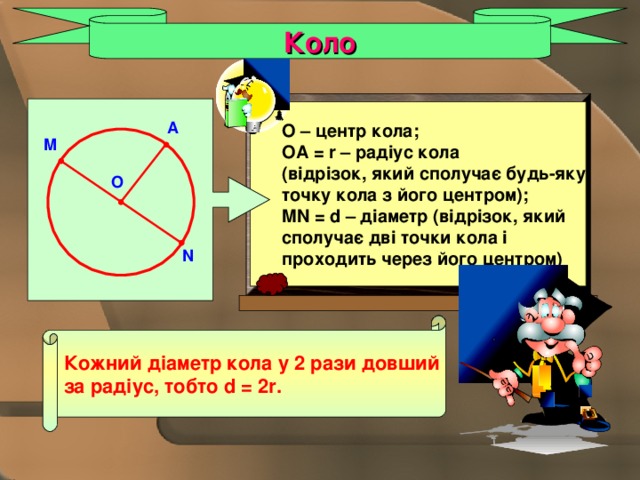
Коло
О – центр кола;
ОА = r – радіус кола
(відрізок, який сполучає будь-яку
точку кола з його центром);
MN = d – діаметр (відрізок, який
сполучає дві точки кола і
проходить через його центром)
A
M
O
N
Кожний діаметр кола у 2 рази довший
за радіус, тобто d = 2 r .

Довжина кола
r
O
≈ 3,14
це відношення довжини кола до діаметра
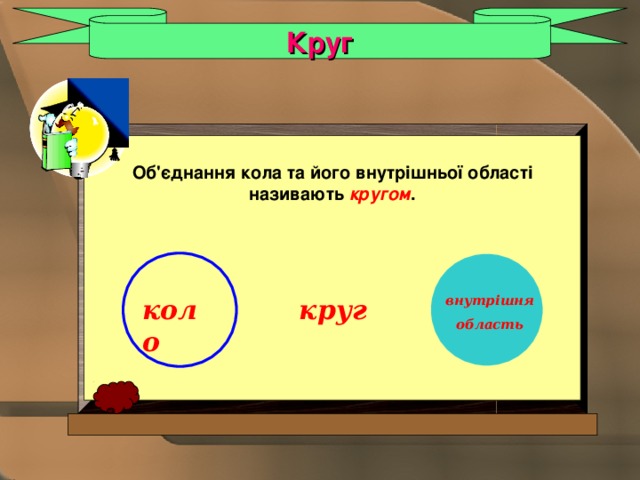
Круг
Об'єднання кола та його внутрішньої області
називають кругом .
внутрішня
область
коло
круг

Площа круга
r
O

Круговий сектор
Частина круга, обмежена двома його радіусами,
називається круговим сектором .
r
r
O

Стовпчасті
та
кругові
діаграми.

лінійні
кругові
Діаграми
Для наочного зображення числових значень
різних величин використовують діаграми .
Слово “ діаграма ” грецького походження,
що означає “ малюнок ”.
Діаграма – це символічний малюнок, який наочно
ілюструє співвідношення між значеннями величин.
Найчастіше використовують діаграми
стовпчасті

Лінійна діаграма
Лінійна діаграма складається з кількох відрізків.
150
120
3530
Волга
Дунай
Урал
Дн і про
Дон
Дністер
95
3645
85
80
3542
73
3750
3560
3900
175 180 185 190 195 200
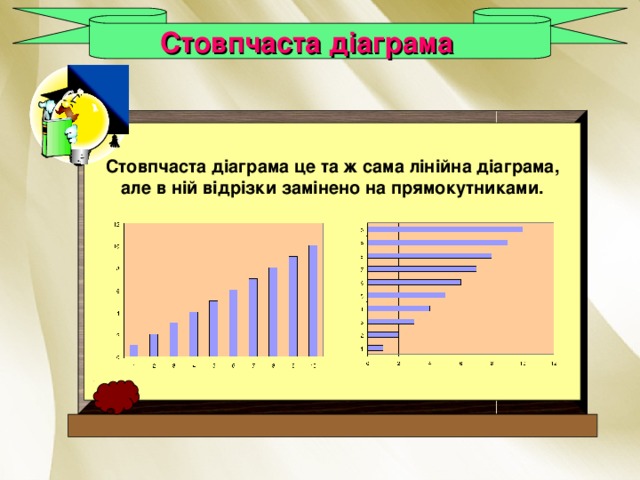
Стовпчаста діаграма
Стовпчаста діаграма це та ж сама лінійна діаграма,
але в ній відрізки замінено на прямокутниками.

Кругова діаграма
Кругова діаграма має вигляд круга, поділеного
радіусами на частини (сектори). Тому такі діаграми
називають також секторними.
 -80%
-80%
 0
0 1323
1323 85
85 Нравится
0
Нравится
0